��Ŀ����
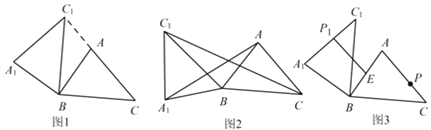
����Ŀ��������ѧϰ������ѧ��- -����Ҫ��������������Խ������������ؽ�ϣ��о��������Ƿ�����������Ҫ�Ĺ��ɣ������ϵ�![]() ����
����![]() ��ʾ����Ϊ
��ʾ����Ϊ![]() ����
����![]() ����֮��ľ���
����֮��ľ���![]() ����
����![]() ����ɼ�Ϊ��
����ɼ�Ϊ��![]() �߶�
�߶�![]() ���е�
���е�![]() ��ʾ����Ϊ
��ʾ����Ϊ![]() ��ͼ����֪��������
��ͼ����֪��������![]() ���㣬�ֱ��ʾ����Ϊ
���㣬�ֱ��ʾ����Ϊ![]() ����
����![]() ��ÿ��
��ÿ��![]() ����λ���ȵ��ٶ����������������˶�����
����λ���ȵ��ٶ����������������˶�����![]() ��ÿ��
��ÿ��![]() ����λ�������������˶������˶�ʱ��Ϊ
����λ�������������˶������˶�ʱ��Ϊ![]() ��
��![]() ��
��
��1���˶���ʼǰ��![]() ����ľ���Ϊ���ٸ���λ���ȣ��߶�
����ľ���Ϊ���ٸ���λ���ȣ��߶�![]() ���е�
���е�![]() ����ʾ����Ϊ��
����ʾ����Ϊ��
��2����![]() �˶�
�˶�![]() �������λ�õĵ��ʾ����Ϊ ����
�������λ�õĵ��ʾ����Ϊ ���� ![]() �˶�
�˶�![]() �������λ�õĵ��ʾ����Ϊ �� (�ú�
�������λ�õĵ��ʾ����Ϊ �� (�ú�![]() ��ʽ�ӱ�ʾ
��ʽ�ӱ�ʾ
��3�����ǰ�������ʽ�˶���![]() ���㾭������������
���㾭������������![]() ����λ����?
�������?
��4����![]() ��������ʽ�˶���
��������ʽ�˶��� ![]() ���㾭�������룬�߶�
���㾭�������룬�߶�![]() ���е�
���е�![]() ��ԭ���غ�?
��ԭ���غ�?
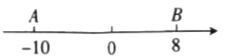
���𰸡���1��18��-1����2��-10+3t��8-2t����3��2.8���4.4������4����λ���ȣ���4������2��A��B������е�M����ԭ���غ�
��������
��1������������ص㼰�е�Ķ��弴����⣻
��2�����ݵ�![]() ��ÿ��
��ÿ��![]() ����λ���ȵ��ٶ����������������˶�����
����λ���ȵ��ٶ����������������˶�����![]() ��ÿ��
��ÿ��![]() ����λ�������������˶�����д��.
����λ�������������˶�����д��.
��3�����������������ۼ�����⣻
��4�����������ú�t��ʽ�ӱ�ʾ�е�M���������.
��1���˶���ʼǰ,![]() ����ľ���Ϊ
����ľ���Ϊ![]() ;�߶�
;�߶�![]() ���е�
���е�![]() ����ʾ��Ϊ
����ʾ��Ϊ
![]()
�ʴ�Ϊ��18��![]() ��
��
��2���ߵ�![]() ��ÿ��
��ÿ��![]() ����λ���ȵ��ٶ����������������˶�����
����λ���ȵ��ٶ����������������˶�����![]() ��ÿ��
��ÿ��![]() ����λ�������������˶�
����λ�������������˶�
���![]() �˶�
�˶�![]() �������λ�õĵ��ʾ����Ϊ
�������λ�õĵ��ʾ����Ϊ![]() ����
���� ![]() �˶�
�˶�![]() �������λ�õĵ��ʾ����Ϊ
�������λ�õĵ��ʾ����Ϊ![]() ��
��
�ʴ�Ϊ��-10+3t��8-2t
![]() �����ǰ�������ʽ�˶�,
�����ǰ�������ʽ�˶�,![]() ���㾭��
���㾭��![]() ������
������![]() �������.���������
�������.���������![]() ��
��![]()
���![]() ��
��![]() .
.
��:![]() ���㾭��
���㾭��![]() ���
���![]() ������
������![]() �������.
�������.
![]() ��������е�MΪ
��������е�MΪ![]() ��
��
����![]()
���![]() .
.
��:����![]() ��
��![]() ������е�
������е�![]() ����ԭ���غ�.
����ԭ���غ�.

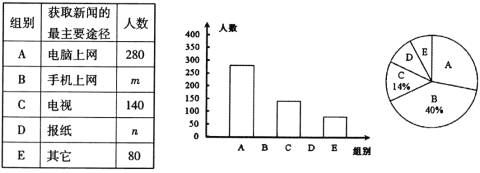
����Ŀ��ijУ������ǿ��ë������ƹ���������������������˶���ÿλͬѧ������ֻ��ѡ��һ�������˶����Ը�Уѧ�������ȡ![]() ���е��飬���ݵ�������������ͼ��������Ƶ���ֲ���������ͳ��ͼ��
���е��飬���ݵ�������������ͼ��������Ƶ���ֲ���������ͳ��ͼ��
�˶���Ŀ | Ƶ�� |
��� | 30 |
���� | a |
ƹ���� | 36 |
���� | b |
���� | 12 |
���������ͼ����Ϣ����������⣺
![]() Ƶ���ֲ����е�
Ƶ���ֲ����е�![]() ______��
______��![]() ______��
______��
![]() ������ͳ��ͼ�У������������ڵ����ε�Բ�Ľ�Ϊ______�ȣ�
������ͳ��ͼ�У������������ڵ����ε�Բ�Ľ�Ϊ______�ȣ�
![]() ȫУ�ж�����ѧ��ѡ��μ�ƹ�����˶���
ȫУ�ж�����ѧ��ѡ��μ�ƹ�����˶���