Question

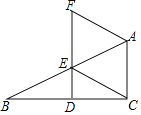
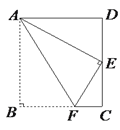
【题目】如图，四边形ABCD为矩形纸片，把纸片ABCD折叠，使点B恰好落在CD边的中点E处, 折痕为AF，若CD=6，则AF等于__________.

Answer 1

【答案】4

【解析】分析：由图形折叠的性质得到BF=EF，AE=AB，再由E是CD的中点可求出ED的长，再求出∠EAD的度数，设FE=x，则AF=2x，在△AFE中利用勾股定理即可求解．

详解：由折叠的性质得BF=EF，AE=AB，

∵CD=6，E为CD中点，

∴ED=3，

在Rt△ADE中，

∵AE=AB=CD=6，

∴DE=AE,

∴∠EAD=30°，

∴∠FAE= (90°30°)=30°，

在Rt△AFE中，

设FE=x，则AF=2x，

,根据勾股定理得，

，

即(2x)2=62+x2，

解得，,x1=2，x2=2 (舍去).

∴AF=2x=4.

故答案为：4.