题目内容
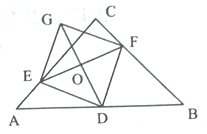
【题目】如图，四边形OABC是平行四边形，边OC在x轴的负半轴上，反比例y= 
（k＜0）的图象经过点A与BC的中点F，连接AF、OF，若△AOF的面积为9，则k的值为 ． 
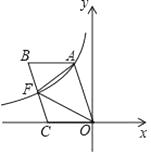
【答案】-9
【解析】解：∵△AOF的面积为9，四边形OABC是平行四边形， ∴△BOC的面积是9，
∵反比例y= 
（k＜0）的图象经过点A与BC的中点F，
∴△OCF的面积是4.5，
∵点F在反比例函数y= （k＜0）的图象上，
∴k=﹣（4.5×2）=﹣9，
所以答案是：﹣9．
【考点精析】利用比例系数k的几何意义和平行四边形的性质对题目进行判断即可得到答案，需要熟知几何意义：表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积；平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分．
练习册系列答案
相关题目
【题目】某校初三（1）班的同学踊跃为“希望工程”捐款，根据捐款情况（捐款数为正数）制作以下统计图表，但班长不小心把墨水滴在统计表上，部分数据看不清楚．根据图表中现有信息解决下列问题：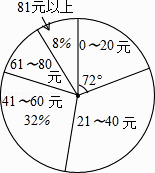 
捐款 | 人数 |
0～20元 | |
21～40元 | |
41～60元 | |
61～80元 | 6 |
81元以上 | 4 |
（1）全班有多少人捐款？
（2）如果捐款0～20元的人数在扇形统计图中所占的圆心角为72°，那么捐款21～40元的有多少人？
