��Ŀ����
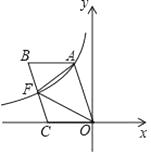
����Ŀ����ͼ����ֱ֪��y= ![]() x��2��x�ύ�ڵ�A����y�ύ�ڵ�C������A��C��������������ύ����һ��B��1��0����
x��2��x�ύ�ڵ�A����y�ύ�ڵ�C������A��C��������������ύ����һ��B��1��0����
��1����������ߵĽ���ʽ��
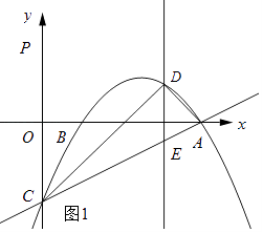
��2����ֱ��y= ![]() x��2�Ϸ����������ϴ���һ����D������AD��CD�����D�ĺ�����Ϊm����DCA�����ΪS����S��m�ĺ�����ϵʽ�������S�����ֵ��
x��2�Ϸ����������ϴ���һ����D������AD��CD�����D�ĺ�����Ϊm����DCA�����ΪS����S��m�ĺ�����ϵʽ�������S�����ֵ��
��3�������������Ƿ����һ��M��ʹ����MΪԲ�ģ��� ![]() Ϊ�뾶��Բ��ֱ��AC���У������ڣ��������M�����ꣻ�������ڣ���˵�����ɣ�
Ϊ�뾶��Բ��ֱ��AC���У������ڣ��������M�����ꣻ�������ڣ���˵�����ɣ�
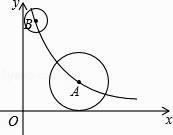
��4����y����������ϴ���һ��P��ʹ��APB��ֵ�����ֱ��д������APB���ʱ��P�����꣮
���𰸡�
��1��
�⣺��x=0����y= ![]() x��2�ã�y=��2��
x��2�ã�y=��2��
��C��0����2����
��y=0����ã� ![]() x��2=0����ã�x=4��
x��2=0����ã�x=4��
��A��4��0����
�������ߵĽ���ʽΪy=a��x��4����x��1��������C���������ã�4a=��2����ã�a=�� ![]() ��
��
�������ߵĽ���ʽΪy=�� ![]() x2+
x2+ ![]() x��2��
x��2��
��2��
�⣺����D��y���ƽ���߽�AC��E�����D��m���� ![]() m2+
m2+ ![]() m��2����E��m��
m��2����E��m�� ![]() m��2����
m��2����
��DE=�� ![]() m2+
m2+ ![]() m��2����
m��2���� ![]() m��2��=��
m��2��=�� ![]() m2+2m��
m2+2m��
���DAC�����S= ![]() ��4������
��4������ ![]() m2+2m��=��m2+4m��
m2+2m��=��m2+4m��
�൱m=2ʱ��S�����ֵΪ4��
��S��m�Ĺ�ϵʽΪS=��m2+4m����DCA��������Ϊ4��
��3��
�⣺�ߡ�M��AC���У�
���AMC��AC���ϵĸ�Ϊ ![]() ��
��
��AC=2��OA=4��
��AC=2 ![]() ��
��
��S��ACM= ![]() ��2
��2 ![]() ��
�� ![]() =4��
=4��
����M��AC����ʱ���ɣ�2����֪����m=2��
���M��������2��1����
����M��AC���·�ʱ������M��y���ƽ���߽�AC��E�����M��m���� ![]() m2+
m2+ ![]() m��2����E��m��
m��2����E��m�� ![]() m��2����
m��2����
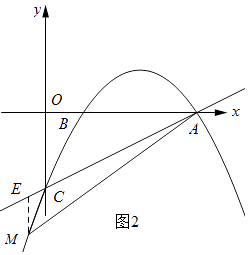
��ME=�� ![]() m��2��������
m��2�������� ![]() m2+
m2+ ![]() m��2��=
m��2��= ![]() m2��2m��
m2��2m��
���MAC�����S= ![]() ��4����
��4���� ![]() m2��2m��=m2��4m��
m2��2m��=m2��4m��
��m2��4m=4�������ã�m2��4m��4=0����ã�m=2+2 ![]() ��m=2��2
��m=2��2 ![]() ��
��
���M��������2+2 ![]() ��
�� ![]() ��3����2��2
��3����2��2 ![]() ����
���� ![]() ��3����
��3����
��4��
�⣺��ͼ3��ʾ������A��AE��PB������ΪE��
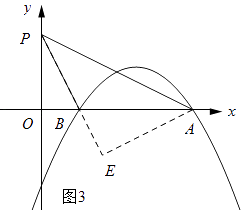
���P������Ϊ��0��a�������ݹ��ɶ����ã�AP= ![]() ��
��
��ֱ��BP�Ľ���ʽΪy=kx+a������B���������ã�k+a=0����ã�k=��a��
��ֱ��PB�Ľ���ʽΪy=��ax+a��
��ֱ��AE�Ľ���ʽΪy= ![]() x+b������A���������ã�
x+b������A���������ã� ![]() +b=0����ã�b=��
+b=0����ã�b=�� ![]() ��
��
��ֱ��AE�Ľ���ʽΪy= ![]() x��
x�� ![]() ��
��
��y=��ax+a��y= ![]() x��
x�� ![]() ��������ã�x=
��������ã�x= ![]() ��y=
��y= ![]() ��
��
���E�������� ![]() ��
�� ![]() ����
����
��AE= ![]() ��
��
��sin��APB= ![]() ��
��
��sin2��APB= 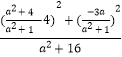 =
= ![]() =
= ![]() =
= ![]() ��
��
��a2+ ![]() ��2��a
��2��a ![]() =8��
=8��
�൱a= ![]() ʱ��sin��APB�����ֵ�����a=2��a=��2����ȥ����
ʱ��sin��APB�����ֵ�����a=2��a=��2����ȥ����
�൱a=2ʱ����APB�����ֵ��
��P��0��2����
����������1�������C��0����2����A��4��0�����������ߵĽ���ʽΪy=a��x��4����x��1��������C�������������a��ֵ����2������D��y���ƽ���߽�AC��E�����D��m���� ![]() m2+
m2+ ![]() m��2����E��m��
m��2����E��m�� ![]() m��2������DE=��
m��2������DE=�� ![]() m2+2m��Ȼ�����������ε������ʽ�ɵõ�S��m�ĺ�����ϵʽ��Ȼ�����ö��κ��������ʿɵõ���DCA����������ֵ����3�������ݹ��ɶ��������AC�ij���Ȼ��ɵõ���ACM�����=4������M��AC����ʱ���ɣ�2����֪M��2��1��������M��AC���·�ʱ������M��y���ƽ���߽�AC��E�����M��m����
m2+2m��Ȼ�����������ε������ʽ�ɵõ�S��m�ĺ�����ϵʽ��Ȼ�����ö��κ��������ʿɵõ���DCA����������ֵ����3�������ݹ��ɶ��������AC�ij���Ȼ��ɵõ���ACM�����=4������M��AC����ʱ���ɣ�2����֪M��2��1��������M��AC���·�ʱ������M��y���ƽ���߽�AC��E�����M��m���� ![]() m2+
m2+ ![]() m��2����E��m��
m��2����E��m�� ![]() m��2������ME=
m��2������ME= ![]() m2��2m��Ȼ��ɵõ�S��m�ĺ�����ϵʽ����s=4��������m��ֵ���Ӷ��õ���M�����ꣻ��4������A��AE��PB������ΪE�����P������Ϊ��0��a�������ݹ��ɶ����ã�AP=
m2��2m��Ȼ��ɵõ�S��m�ĺ�����ϵʽ����s=4��������m��ֵ���Ӷ��õ���M�����ꣻ��4������A��AE��PB������ΪE�����P������Ϊ��0��a�������ݹ��ɶ����ã�AP= ![]() ��Ȼ�������BP��AE�Ľ���ʽ���Ӷ�����õ�E�����꣬Ȼ����sin��APB=
��Ȼ�������BP��AE�Ľ���ʽ���Ӷ�����õ�E�����꣬Ȼ����sin��APB= ![]() ���õ�sin2��APB
���õ�sin2��APB ![]() ���ʴ˵�a=
���ʴ˵�a= ![]() ʱ��sin��APB�����ֵ���Ӷ������a��ֵ��
ʱ��sin��APB�����ֵ���Ӷ������a��ֵ��
�����㾫�������ڱ��⿼��Ķ��κ�����ͼ��Ͷ��κ��������ʣ���Ҫ�˽���κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С���ܵó���ȷ�𰸣�