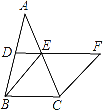
题目内容
【题目】已知:如图,在△ABC中,D、E、F分别是各边的中点,AH是高,求证:∠DHF=∠DEF.

【答案】证明见解析.
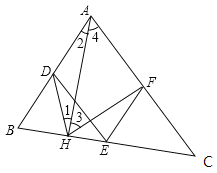
【解析】分析:在△ABH中,根据直角三角形斜边上的中线等于斜边的一半可得DH=![]() AB=AD,从而得到∠1=∠2,同理可证出∠3=∠4,从而得到∠DHF=∠DAF,再利用三角形的中位线定理证明四边形ADEF是平行四边形,可得到∠DAF=∠DEF,即可证出∠DHF=∠DEF.
AB=AD,从而得到∠1=∠2,同理可证出∠3=∠4,从而得到∠DHF=∠DAF,再利用三角形的中位线定理证明四边形ADEF是平行四边形,可得到∠DAF=∠DEF,即可证出∠DHF=∠DEF.
详解:如图.∵AH⊥BC于H,
又∵D为AB的中点,
∴DH=![]() AB=AD,
AB=AD,
∴∠1=∠2,
同理可证:∠3=∠4,
∴∠1+∠3=∠2+∠4,
即∠DHF=∠DAF,
∵E、F分别为BC、AC的中点,
∴EF∥AB且EF=![]() AB,
AB,
即EF∥AD且EF=AD,
∴四边形ADEF是平行四边形,
∴∠DAF=∠DEF,
∴∠DHF=∠DEF.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目