题目内容
【题目】如图，△ABC中，点O是AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．
（1）判断OE与OF的大小关系？并说明理由？
（2）当点O运动何处时，四边形AECF是矩形？并说出你的理由．
【答案】（1）证OE=OC，OF=OC，推出OE=OF，
（2）当点O运动到AC的中点时，四边形AECF是矩形
【解析】试题分析：
(1)先判断∠ECF=90°，再利用角平分线，平行线，等腰三角形的关系得到OE=OC，OF=OC；
(2)结合(1)中的结论，利用对角线相等的平行四边形是矩形说明.
试题解析：
(1)OE=OF，理由如下：
∵CE，CF分别是∠ACB和∠ACB外角的平分线，
∴∠ACE=∠BCE=
∠ACB，∠ACF=∠GCF=∠ACG.
∴∠ECF=∠ACE+∠ACF=∠ACB+∠ACG=(ACB+∠ACG)=∠BCG=90°.
∵MN∥BC，∴∠FEC=∠BCE，∴∠FEC=∠ACE，∴OE=OC.
同理OF=OC，所以OE=OF.
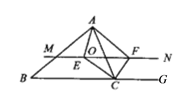
(2)由(1)得，OC=OE=OF，所以当OA=OC时，对角线AC与EF互相平分且相等，而对角线相等的平行四边形是矩形，则当点O运动到AC的中点时，四边形AECF是矩形.
练习册系列答案
相关题目
