题目内容
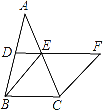
【题目】如图，在△ABC中，D、E分别是AB、AC的中点，BE=2DE，延长DE到点F，使得EF=BE，连接CF．
（1）求证：四边形BCFE是菱形；
（2）若CE=4，∠BCF=120°，求菱形BCFE的面积．
【答案】（1）证明见解析； （2）菱形的面积为8
．
【解析】试题分析：（1）从所给的条件可知，DE是△ABC中位线，所以DE∥BC且2DE=BC，所以BC和EF平行且相等，所以四边形BCFE是平行四边形，又因为BE=FE，所以是菱形；
（2）∠BCF是120°，所以∠EBC为60°，所以菱形的边长也为4，求出菱形的高面积就可求．
试题解析：（1）证明：∵D、E分别是AB、AC的中点，∴DE∥BC且2DE=BC．又∵BE=2DE，EF=BE，∴EF=BC，EF∥BC，∴四边形BCFE是平行四边形．又∵BE=FE，∴四边形BCFE是菱形；
（2）解：∵∠BCF=120°，∴∠EBC=60°，∴△EBC是等边三角形，∴菱形的边长为4，高为2
，∴菱形的面积为4×2
=8
．
练习册系列答案
相关题目
