题目内容
【题目】如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=4,EF=8,FC=12,则正方形与其外接圆形成的阴影部分的面积为 . 
【答案】80π﹣160
【解析】解:连接AC,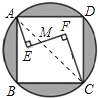
∵AE丄EF,EF丄FC,
∴∠E=∠F=90°,
∵∠AME=∠CMF(对顶角相等),
∴△AEM∽△CFM,
∴ ![]() ,
,
∵AE=4,FC=12,
∴ ![]() ,
,
∴EM=2,FM=6,
在Rt△AEM中,AM= ![]() =2
=2 ![]() ,在Rt△FCM中,CM=
,在Rt△FCM中,CM= ![]() =6
=6 ![]() ,∴AC=8
,∴AC=8 ![]() ,在Rt△ABC中,AB=ACsin45°=8
,在Rt△ABC中,AB=ACsin45°=8 ![]() ×
× ![]() =4
=4 ![]() ,
,
∴S正方形ABCD=AB2=160,
圆的面积为:π( ![]() )2=80π,
)2=80π,
∴正方形与其外接圆之间形成的阴影部分的面积为80π﹣160.
所以答案是:80π﹣160.
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握正方形的性质(正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形)的相关知识才是答题的关键.

练习册系列答案
相关题目





