题目内容
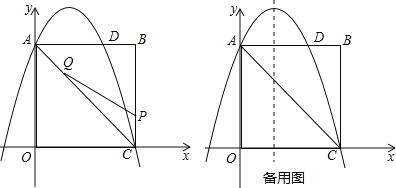
【题目】如图,在平面直角坐标系中,B(5,0),点A在第一象限,且OA=OB,sin∠AOB=![]() .
.
(1)求过点O,A,B三点的抛物线的解析式.
(2)若y=![]() 的图象过(1)中的抛物线的顶点,求k的值.
的图象过(1)中的抛物线的顶点,求k的值.
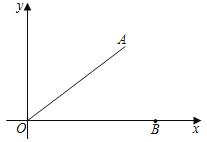
【答案】(1)y=﹣![]() x2+
x2+![]() x;(2)
x;(2)![]() .
.
【解析】
(1)根据题意求得A(4,3),然后根据待定系数法即可求得抛物线的解析式;
(2)把解析式化成顶点式,求得顶点坐标,代入y=![]() ,即可求得k的值.
,即可求得k的值.
解:(1)由题意得OA=OB=5,
作AH⊥x轴于H,则AH=OAsin∠AOB=3,
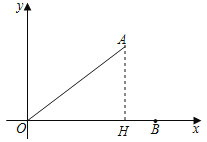
∴OH=4,
∴A(4,3),
设过O、A、B三点的抛物线为y=ax(x﹣5),
把A(4,3)代入得,3=4a(4﹣5),解得a=![]() ,
,
∴过点O,A,B三点的抛物线的解析式为y=![]() x(x﹣5),
x(x﹣5),
即y=﹣![]() x2+
x2+![]() x;
x;
(2)∵y=![]() x2+
x2+![]() x=
x=![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
∴抛物线的顶点为(![]() ,
,![]() ),
),
∵y=![]() 的图象过抛物线的顶点,
的图象过抛物线的顶点,
∴k=![]() ×
×![]() =
=![]() .
.

练习册系列答案
相关题目