题目内容
【题目】已知等腰直角△ABC，∠C=90°，AC=2，D为边AC上一动点，连结BD，在射线BD上取一点E使BEBD=AB2．若点D由A运动到C，则点E运动的路径长为_____．
【答案】π
【解析】
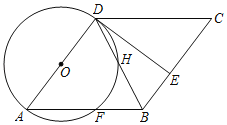
延长BC至点F，使得BC=CF，以点C为圆心，以CF为半径，作⊙C，根据相似三角形的判定与性质可知∠BFA=∠BEA=45°，从而可知点A、B、F、E四点共圆，点E在
上运动，利用弧长公式即可求得E的运动路径长．
延长BC至点F，使得BC=CF，
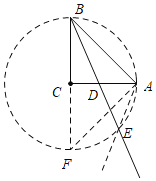
以点C为圆心，以CF为半径，作⊙C，
∵BEBD=AB2，
∴
，
∵∠DBA=∠ABE，
∴△ABD∽△EBA，
∴∠BAD=∠AEB=45°，
∵∠BFA=45°，
∴∠BFA=∠BEA=45°，
∴点A、B、F、E四点共圆，
∵点D在AC上运动，
∴点E在上运动，
∴弧AF的长为：
，
故答案为：π．
练习册系列答案
相关题目
【题目】某体育用品商店购进了足球和排球共20个，一共花了1360元，进价和售价如表：
足球 | 排球 | |
进价（元/个） | 80 | 50 |
售价（元/个） | 95 | 60 |
（l）购进足球和排球各多少个？
（2）全部销售完后商店共获利润多少元？
