题目内容
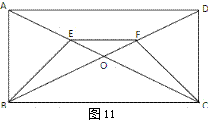
（11·湖州）如图，已知梯形ABCD，AD∥BC，对角线AC，BD相交于点O，
△AOD与△BOC的面积之比为1：9，若AD=1，则BC的长是▲。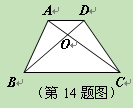
△AOD与△BOC的面积之比为1：9，若AD=1，则BC的长是▲。
3
根据AD∥BC，求证△AOD∽△BOC，再利用相似三角形面积的比等于相似比的平方即可求得答案．
解：∵AD∥BC，
∴△AOD∽△BOC，
∵△AOD与△BOC的面积之比为1：9，
∴
，
∵AD=1，
∴BC=3．
故答案为：3．
解：∵AD∥BC，
∴△AOD∽△BOC，
∵△AOD与△BOC的面积之比为1：9，
∴
，∵AD=1，
∴BC=3．
故答案为：3．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
，
，
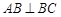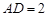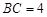，点E在AB边上，且C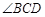E平分
，DE平分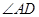
，则点E到CD的距离为 ．
