题目内容
【题目】
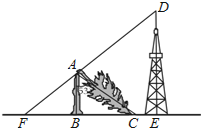
如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.

(1)判断AB、AE的数量关系,并说明理由;
(2)求两个岛屿A和B之间的距离(结果精确到0.1km).
(参考数据:≈1.73,sin74°≈,cos74°≈0.28,tan74°≈3.49,sin76°≈0.97,cos76°≈0.24)
【答案】
(1)相等
(2)3.6
【解析】(1)相等,
证明:∵∠BEQ=30°,∠BFQ=60°,∴∠EBF=30°,∴EF=BF.
又∵∠AFP=60°,∴∠BFA=60°.
在△AEF与△ABF中,EF=BF,∠AFE=∠AFB,AF=AF,∴△AEF≌△ABF,∴AB=AE.
(2)法一:作AH⊥PQ,垂足为H,设AE=x,
则AH=xsin74°,HE=xcos74°,HF=xcos74°+1.
Rt△AHF中,AH=HF·tan60°,∴xcos74°=(xcos74°+1)·tan60°,即0.96x=(0.28x+1)×1.73,
∴x≈3.6,即AB≈3.6 km.答:略.
法二:设AF与BE的交点为G,在Rt△EGF中,∵EF=1,∴EG=![]() .
.
在Rt△AEG中,∠AEG=76°,AE=EG÷cos76°=![]() ÷0.24≈3.6.
÷0.24≈3.6.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目