题目内容
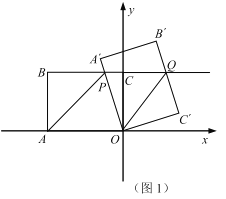
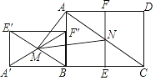
【题目】如图,已知矩形ABCD满足AB:BC=1: ![]() ,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )
,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )
A. 4 ![]() B. 4 C. 2 D. 1
B. 4 C. 2 D. 1
【答案】C
【解析】
先根据已知条件判定△E'A'B∽△ABC,得出∠A'BE'=∠ACB,进而判定AC∥BE',连接BN,则△AMN的面积=△ABN的面积,根据N为AC的中点,故△ABN的面积为△ABC面积的一半,进而得到△AMN的面积为△ABC面积的一半,即矩形ABCD面积的四分之一,据此可得结论.
如图:
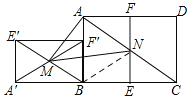
由折叠可得,BE=![]() BC=AF,而AB:BC=1:
BC=AF,而AB:BC=1:![]() ,
,
∴![]() ,
,
由旋转可得,AF=A'E',AB=A'B,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵∠E'A'B=∠ABC=90°,
∴△E'A'B∽△ABC,
∴∠A'BE'=∠ACB,
∴AC∥BE',
连接BN,则△AMN的面积=△ABN的面积,
由题可得,N为AC的中点,故△ABN的面积为△ABC面积的一半,
∴△AMN的面积为△ABC面积的一半,即矩形ABCD面积的四分之一,
∴△AMN的面积=![]() ×8=2,
×8=2,
故选:C.

练习册系列答案
相关题目