题目内容
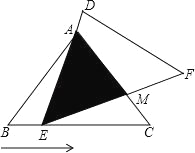
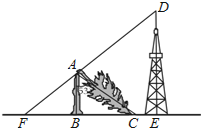
【题目】如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成53°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33)
【答案】这棵大树没有折断前的高度为10.8米.
【解析】试题分析:由题意得出AB∥DE,证出△ABF∽△DEF,由相似三角形的性质得出![]() ,求出AB,再由三角函数求出AC,即可得出结果.
,求出AB,再由三角函数求出AC,即可得出结果.
试题解析:根据题意得:AB⊥EF,DE⊥EF,
∴∠ABC=90°,AB∥DE,
∴△ABF∽△DEF,
∴![]() ,即
,即![]() ,
,
解得:AB=3.6,
∵cos∠BAC=![]() ,
,
∴AC=![]() =7.2米,
=7.2米,
∴AB+AC=3.6+7.2=10.8米.
答:这棵大树没有折断前的高度为10.8米.

练习册系列答案
相关题目
【题目】某班同学上学期全部参加了捐款活动,捐款情况如下统计表:
金额(元) | 5 | 10 | 15 | 20 | 25 | 30 |
人数(人) | 8 | 12 | 10 | 6 | 2 | 2 |
(1)求该班学生捐款额的平均数和中位数;
(2)试问捐款额多于15元的学生数是全班人数的百分之几?
(3)已知这笔捐款是按3:5:4的比例分别捐给灾区民众、重病学生、孤老病者三种被资助的对象,问该班捐给重病学生是多少元?