题目内容
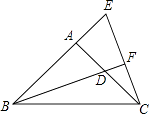
【题目】如图,在等边△ABC中,M为BC边上的中点,D是射线AM上的一个动点,以CD为一边且在CD的下方作等边△CDE,连接BE. 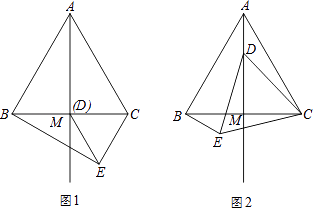
(1)填空:若D与M重合时(如图1)∠CBE=度;
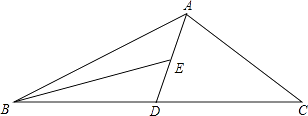
(2)如图2,当点D在线段AM上时(点D不与A、M重合),请判断(1)中结论是否成立?并说明理由;
(3)在(1)的条件下,若AB=6,试求CE的长.
【答案】
(1)30
(2)解:(1)中结论成立.理由如下:
如图2.
∵△ABC和△CDE均为等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD+∠DCB=∠DCB+∠BCE=60°,
∴∠ACD=∠BCE.
在△ACD与△BCE中,
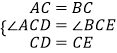 ,
,
∴△ACD≌△BCE,
∴∠CAD=∠CBE,
∵在等边△ABC中,M是BC中点.
∴∠CAD= ![]() ∠BAC=30°,
∠BAC=30°,
∴∠CBE=30°
(3)解:如图1.
∵在等边△ABC中,AB=6,
∴BC=AB=6.
∵在等边△ABC中,M为BC边上的中点,D与M重合,
∴CD=BD= ![]() BC=3,
BC=3,
∵△CDE是等边三角形,
∴CE=CD=3.
【解析】解:(1)如图1.
∵在等边△ABC中,M为BC边上的中点,D与M重合,
∴BD=CD,
∵△CDE是等边三角形,
∴∠CDE=60°,CD=DE,
∴BD=DE,
∴∠BED=∠DBE,
又∵∠BED+∠DBE=∠CDE=60°,
∴∠DBE=30°,即∠CBE=30°;
所以答案是30;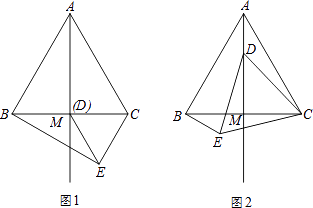
【考点精析】本题主要考查了等边三角形的性质的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°才能正确解答此题.

练习册系列答案
相关题目