题目内容
【题目】（12分）为绿化环境，汇川区园林局引进了A、B两种树苗，若购进A种树苗4棵，B种树苗2棵，需要1600元；若购进3棵A种树苗，4棵B种树苗，需1700元，问：
（1）A、B两种树苗的单价各是多少？
（2）若计划不超过8300元购进A、B两种树苗共30棵，其中计划A种树苗至少比B种树苗的2倍多2棵，问有几种采购方案？那种方案最节约？
【答案】(1) A树苗每棵300元，B种树苗每棵200元;(2) 有3种方案,其中B种树苗9棵，A种树苗21棵，最节约.
【解析】试题分析：（1）设A种树苗每棵x元，B种树苗每棵y元，根据“若购进A种树苗4棵，B种树苗2棵，需要1600元；若购进3棵A种树苗，4棵B种树苗，需1700元”，即可得出关于x、y的二元一次方程组，解之即可得出结论；
（2）设购进A种树苗m棵，则购进B种树苗（30-m）棵，根据购树费用不超过8300元结合A种树苗至少比B种树苗的2倍多2棵，即可得出关于m的一元一次不等式组，解之即可得出m的取值范围，从而得出各购树方案，再根据一次函数的性质，即可解决最值问题．
试题解析：
（1）设A种树苗每棵x元，B种树苗每棵y元，则：
解这个方程组，得： 
答：A树苗每棵300元，B种树苗每棵200元。
（2）解法一：设购进A种树苗m棵，则购进B种树苗（30-m）棵，由题意，得：
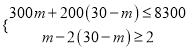
解这个不等式组，得： 
又 m是整数，∴m=21、22或23
故有3种方案：A种树苗21棵，B种树苗9棵
A种树苗22棵，B种树苗8
A种树苗23棵，B种树苗7棵
由购树费用=
知，m最小时最合算，
∴ 方案一：A种树苗21棵，B种树苗9棵，最节约
或解法二：设购进B种树苗t棵，则有：
解得： 
t是整数，∴t=7、8或9
B种树苗9棵，A种树苗21棵，最节约.
