题目内容
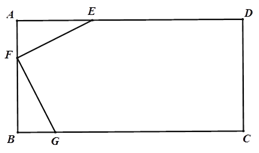
【题目】如图,有一块矩形板材ABCD,AB=3米,AD=6米,E,F,G分别在AD,AB,BC上,∠EFG=900,EF=FG=![]() 米,AF<BF.现想从此板材中剪出一个四边形EFGH,使得∠EHG=450,则四边形EFGH面
米,AF<BF.现想从此板材中剪出一个四边形EFGH,使得∠EHG=450,则四边形EFGH面
积的最大值是____________平方米.
【答案】![]()
【解析】根据余角的性质得到1=∠2,推出△AEF≌△BGF,根据全等三角形的性质得到![]() 接下来先证明四边形EFGO是正方形,求∠EOG的度数,得到四边形EFGH′是符合条件的最大四边形,根据矩形的面积公式即可得到结论.
接下来先证明四边形EFGO是正方形,求∠EOG的度数,得到四边形EFGH′是符合条件的最大四边形,根据矩形的面积公式即可得到结论.
能裁得,理由:
∵![]()
∴∠1=∠2.
在△AEF与△BGF中,
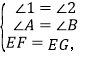
∴△AEF≌△BGF,
∴![]() 设
设![]() ,则
,则![]()
∴![]() 解得:x=1,x=2(不合题意,舍去).
解得:x=1,x=2(不合题意,舍去).
∴![]()
∴![]()
连接EG,作△EFG关于EG的对称△EOG,则四边形EFGO是正方形,∠EOG=90°.
以O为圆心,以OE为半径作⊙O,则使得∠EHG=45°的点在⊙O上.
连接FO,并延长交⊙O于H′,则H′在EG的垂直平分线上,连接EH′、GH′,则∠EH′G=45°,此时,四边形EFGH′是要想裁得符合要求的面积最大的四边形,
∴C在线段EG的垂直平分线上,
∴点F,O,H′,C在一条直线上.
∵![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴OH′<OC,
∴点H′在矩形ABCD的内部.
∴可以在矩形ABCD中,裁得符合条件的面积最大的四边形EFGH′,
其面积=![]()
∴当所裁得的四边形为四边形EFGH′时,裁得了符合条件的最大四边形,其面积为(![]() )m2.
)m2.

故答案为:![]()

 名题金卷系列答案
名题金卷系列答案【题目】某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:
鸭的质量/千克 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
烤制时间/分 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
设鸭的质量为x千克,烤制时间为t,估计当x=2.8千克时,t的值为( )
A. 128B. 132C. 136D. 140