题目内容
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B
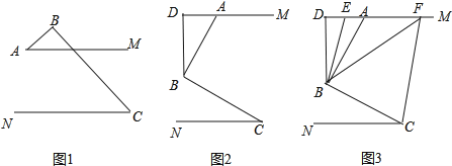
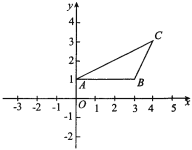
(1)如图1,直接写出∠A和∠C之间的数量关系;
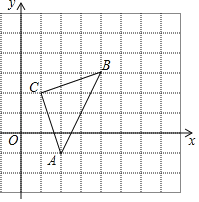
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
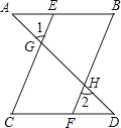
(3)如图3,在(2)问的条件下,点E.F在DM上,连接BE.BF.CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠ABF=2∠ABE,求∠EBC的度数.
【答案】(1)90°;(2)详见解析;(3)105°
【解析】
(1)根据平行线的性质以及直角三角形的性质进行证明即可;
(2)先过点B作BG∥DM,根据同角的余角相等,得出∠ABD=∠CBG,再根据平行线的性质,得出∠C=∠CBG,即可得到∠ABD=∠C;
(3)先过点B作BG∥DM,根据角平分线的定义,得出∠ABF=∠GBF,再设∠DBE=α,∠ABF=β,根据∠CBF+∠BFC+∠BCF=180°,可得(2α+β)+3α+(3α+β)=180°,根据AB⊥BC,可得β+β+2α=90°,最后解方程组即可得到∠ABE=15°,进而得出∠EBC=∠ABE+∠ABC=15°+90°=105°.
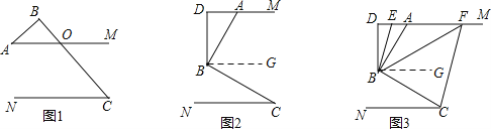
解:(1)如图1,AM与BC的交点记作点O,
∵AM∥CN,
∴∠C=∠AOB,
∵AB⊥BC,
∴∠A+∠AOB=90°,
∴∠A+∠C=90°;
(2)如图2,过点B作BG∥DM,
∵BD⊥AM,
∴DB⊥BG,即∠ABD+∠ABG=90°,
又∵AB⊥BC,
∴∠CBG+∠ABG=90°,
∴∠ABD=∠CBG,
∵AM∥CN,BG∥AM,
∴CN∥BG,
∴∠C=∠CBG,
∴∠ABD=∠C;
(3)如图3,过点B作BG∥DM,
∵BF平分∠DBC,BE平分∠ABD,
∴∠DBF=∠CBF,∠DBE=∠ABE,
由(2)可得∠ABD=∠CBG,
∴∠ABF=∠GBF,
设∠DBE=α,∠ABF=β,则
∠ABE=α,∠ABD=2α=∠CBG,∠GBF=β=∠AFB,∠BFC=3∠DBE=3α,
∴∠AFC=3α+β,
∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,
∴∠FCB=∠AFC=3α+β,
△BCF中,由∠CBF+∠BFC+∠BCF=180°,可得
(2α+β)+3α+(3α+β)=180°,①
由AB⊥BC,可得
β+β+2α=90°,②
由①②联立方程组,解得α=15°,
∴∠ABE=15°,
∴∠EBC=∠ABE+∠ABC=15°+90°=105°.

 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案【题目】一个箱子内有4颗相同的球,将4颗球分别标示号码1、2、3、4,今翔翔以每次从箱子内取一颗球且取后放回的方式抽取,并预计取球10次,现已取了8次,取出的结果如表所列:
次数 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 | 第8次 | 第9次 | 第10次 |
号码 | 1 | 3 | 4 | 4 | 2 | 1 | 4 | 1 |
若每次取球时,任一颗球被取到的机会皆相等,且取出的号码即为得分,请回答下列问题:
(1)请求出第1次至第8次得分的平均数.
(2)承(1),翔翔打算依计划继续从箱子取球2次,请判断是否可能发生「这10次得分的平均数不小于2.2,且不大于2.4」的情形?若有可能,请计算出发生此情形的机率,并完整写出你的解题过程;若不可能,请完整说明你的理由.