题目内容
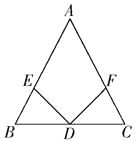
【题目】如图所示,在△ABC中,∠BAC的平分线AD交BC于点D,DE垂直平分AC,垂足为点E,∠BAD=29°,求∠B的度数.

【答案】93°
【解析】试题分析:已知AD平分∠BAC,∠BAD=29°,根据角平分线的定义可得∠BAC=58°;再由DE垂直平分AC,根据线段垂直平分线的性质定理可得AD=DC,根据等腰三角形的性质可得∠DAE=∠DCA=29°,在△ABC中,根据三角形的内角和定理即可求得∠B=93°.
试题解析:
∵AD平分∠BAC
∴∠BAD=∠DAE,
∵∠BAD=29°,
∴∠DAE=29°,
∴∠BAC=58°,
∵DE垂直平分AC,
∴AD=DC,
∴∠DAE=∠DCA=29°,
∵∠BAC+∠C+∠B=180°,
∴∠B=93°.

练习册系列答案
相关题目