Question

【题目】已知：t1，t2是方程t2+2t﹣24＝0的两个实数根，且t1＜t2，抛物线y＝x2+bx+c的图象经过点A（t1，0），B（0，t2）．

（1）求这个抛物线的解析式；

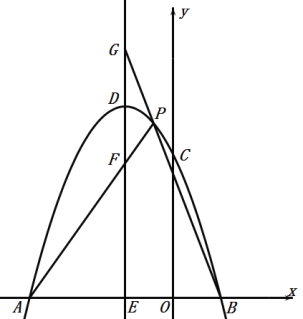
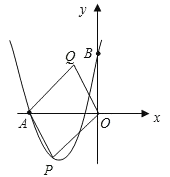
（2）设点P（x，y）是抛物线上一动点，且位于第三象限，四边形OPAQ是以OA为对角线的平行四边形，求平行四边形OPAQ的面积S与x之间的函数关系式，并写出自变量x的取值范围；

（3）在（2）的条件下，当平行四边形OPAQ的面积为24时，是否存在这样的点P，使OPAQ为正方形？若存在，求出P点坐标；若不存在，说明理由．

Answer 1

【答案】（1）y＝x2+x+4；（2）S＝﹣4（x+）2+25（﹣6＜x＜﹣1）；（3）不存在这样的点P，使四边形OPAQ为正方形，理由见解析

【解析】

（1）解方程t2+2t﹣24＝0，可得A(-6,0)，B(0,4)，再利用待定系数法求二次函数的解析式；

（2）设点P（x，y），利用x，y表示四边形的边长求得面积S＝﹣+25，利用面积是正数的性质求出x的取值范围是﹣6＜x＜﹣1；

（3）把S＝24代入解析式S＝﹣+25中求得y的值，从而得到点P的坐标，根据实际意义进行值的取舍，讨论可知不存在这样的点P，使四边形OPAQ为正方形．

解：（1）t2+2t﹣24＝0，（t+6）（t﹣4）＝0，t1＝﹣6，t2＝4

∵t1＜t2，

∴A（﹣6，0），B（0，4）

∵抛物线y＝x2+bx+c经过A，B两点．

∴，

解得，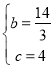

∴y＝x2+x+4．

（2）∵点P（x，y）在抛物线上，位于第三象限，

∴y＜0，即﹣y＞0．

又∵S＝2S△APO＝2××|OA||y|＝|OA||y|＝6|y|，

∴S＝﹣6y

＝﹣6（x2+x+4）

＝﹣4（x2+7x+6）

＝﹣4（x+）2+25

令y＝0时，x2+x+4＝0，

解得x1＝﹣6，x2＝﹣1．

∵抛物线与x轴的交点坐标为（﹣6，0），（﹣1，0），

∴x的取值范围为﹣6＜x＜﹣1．

（3）当S＝24时，得24＝﹣4（x+）2+25，

解得：x1＝﹣3，x2＝﹣4

代入解析式得：y1＝﹣4，y2＝﹣4．

∴点P的坐标为（﹣3，﹣4），（﹣4，﹣4）

当点P为（﹣3，﹣4）时，满足PO＝PA，此时，平行四边形OPAQ是菱形．

当点P为（﹣4，﹣4）时，不满足PO＝PA，此时，平行四边形OPAQ不是菱形．

而要使平行四边形OPAQ为正方形，那么，一定有OA⊥PQ，AO＝PQ，

此时，点P的坐标为（﹣3，﹣3），而（﹣3，﹣3）不在抛物线y＝x2+x+4上，

故不存在这样的点P，使四边形OPAQ为正方形．