��Ŀ����
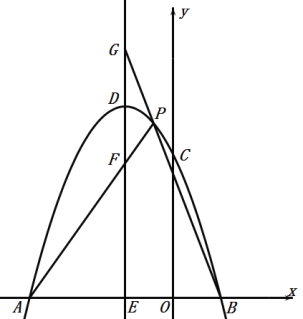
����Ŀ����֪����MΪ���κ���y��x2+2bx+3cͼ��Ķ��㣬һ�κ���y��kx��3��k��0���ֱ�x�ᣬy���ڵ�A��B��
��1����b��1��c��1���ж϶���M�Ƿ���ֱ��y��2x+1�ϣ���˵�����ɣ�
��2�����ö��κ���ͼ����C��1����4����Ҳ������A��B��������kx��3��x2+2bx+3c�����һ�κ�������ʽ����ֱ��д���Ա���x��ȡֵ��Χ��
��3�����P����Ϊ��m��n���ڶ��κ���y��x2+2bx+3c�ϣ�����2��m��2ʱ��b��24��n��2b+4�����ʣ���b��2��b����2ʱ�����ڸö��κ�����������Ա���x������ֵy�Ƿ�ʼ�մ��ک�40����˵�����ɣ�
���𰸡���1��M����ֱ��y��2x+1�ϣ�����������2��y��x2��2x��3��x��3��x��0����3����b��2��b����2ʱ�����ڸö��κ�����������Ա���x������ֵyʼ�մ��ک�40
��������
(1)b��1,c��1ʱ,y��x2+2x+3,���M(��1,2),����M(��1,2)����y��2x+1��֤�Ƿ����㼴�ɣ�
(2)�����֪B(0,��3),C(1,��4),����y��x2+2bx+3c�õ�b����1,c����1,���A(![]() ,0),�ٽ���A������κ�������ʽ�õ�
,0),�ٽ���A������κ�������ʽ�õ�![]() ��
��![]() ��3��0,���k��1��
��3��0,���k��1��
(3)�����Գ���Ϊx����b,�ٵ���b����2ʱ,��b��2,��ʱb��24��4��4b+3c,��5b��3c��28,2b+4��4+4b+3c,��2b+3c��0,���y��x2+8x��8��(x+4)2��24����24����40���ڵ���b��2ʱ,��b����2,��ʱb��24��4+4b+3c,��3b+3c����28,2b+4��4��4b+3c,��6b��3c��0,���y��x2��![]() x��
x��![]() ��(x��
��(x��![]() )2��
)2��![]() ����
����![]() ����40��
����40��
�⣺(1)b��1,c��1ʱ,y��x2+2x+3=(x+1)2+2,
��M(��1,2),
����M(��1,2)����y��2x+1,��1��2,
��M������ֱ��y��2x+1�ϣ�
(2)��B��һ�κ���y=kx-3�ҽ���y��,��x=0,���y=-3,��B(0,-3).
��B(0,��3),C(1,��4),�������y��x2+2bx+3c.
����õ�:![]() ,���:b����1,c����1,
,���:b����1,c����1,
��y��x2��2x��3,
��A��y=kx-3����x��,��y=0,���x=![]() ,��A(
,��A(![]() ,0),
,0),
��![]() ��
��![]() ��3��0,
��3��0,
��k��1��k����3,
��k��0,
��k��1,
��y��x��3,
��x��3��x2��2x��3,
��x��3��x��0��
(3)�����Գ���Ϊx����b,
������b����2ʱ,��b��2,
��ʱb��24��4��4b+3c,��5b��3c��28,
2b+4��4+4b+3c,��2b+3c��0,
��b��4,c����![]() ,
,
��y��x2+8x��8��(x+4)2��24����24����40��
������b��2ʱ,��b����2,��ʱ
b��24��4+4b+3c,��3b+3c����28,
2b+4��4��4b+3c,��6b��3c��0,
��b����![]() ,c����
,c����![]() ,
,
��y��x2��![]() x��
x��![]() ��(x��
��(x��![]() )2��
)2��![]() ����
����![]() ����40��
����40��
����b��2��b����2ʱ,���ڸö��κ�����������Ա���x,����ֵyʼ�մ��ک�40��