题目内容
【题目】在平面直角坐标系中，抛物线y＝x2﹣4x+n（x＞0）的图象记为G1，将G1绕坐标原点旋转180°得到图象G2，图象G1和G2合起来记为图象G．
（1）若点P（﹣1，2）在图象G上，求n的值．
（2）当n＝﹣1时．
①若Q（t，1）在图象G上，求t的值．
②当k≤x≤3（k＜3）时，图象G对应函数的最大值为5，最小值为﹣5，直接写出k的取值范围．
（3）当以A（﹣3，3）、B（﹣3，﹣1）、C（2，﹣1）、D（2，3）为顶点的矩形ABCD的边与图象G有且只有三个公共点时，直接写出n的取值范围．
【答案】（1）n的值为﹣3或1；（2）①t＝2±
或﹣4或0，②﹣2﹣
≤k≤﹣2；（3）当n＝0，n＝5，1＜n＜3时，矩形ABCD的边与图象G有且只有三个公共点．
【解析】
（1）先确定图像G2的顶点坐标和解析式，然后就P分别在图象G1和G2上两种情况讨论求解即可；
（2）①先分别求出图象G1和G2的解析式，然后就P分别在图象G1和G2上两种情况讨论求解即可；
②结合图像如图1，即可确定k的取值范围；
（3）结合图像如图2，根据分n的取值范围分类讨论即可求解．
（1）∵抛物线y＝x2﹣4x+n＝（x﹣2）2+n﹣4，
∴顶点坐标为（2，n﹣4），
∵将G1绕坐标原点旋转180°得到图象G2，
∴图象G2的顶点坐标为（﹣2，﹣n+4），
∴图象G2的解析式为：y＝﹣（x+2）2+4﹣n，
若点P（﹣1，2）在图象G1上，
∴2＝9+n﹣4，
∴n＝﹣3；
若点P（﹣1，2）在图象G2上，
∴2＝﹣1+4﹣n，
∴n＝1；
综上所述：点P（﹣1，2）在图象G上，n的值为﹣3或1；
（2）①当n＝﹣1时，则图象G1的解析式为：y＝（x﹣2）2﹣5，图象G2的解析式为：y＝﹣（x+2）2+5，
若点Q（t，1）在图象G1上，
∴1＝（t﹣2）2﹣5，
∴t＝2±，
若点Q（t，1）在图象G2上，
∴1＝﹣（t+2）2+5，
∴t1＝﹣4，t2＝0
②如图1，
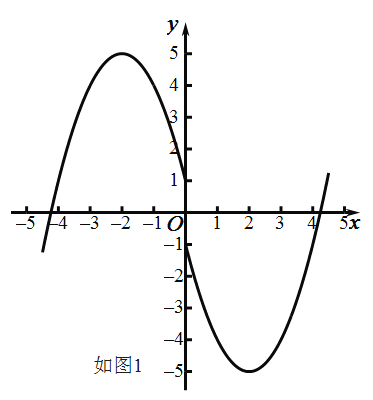
当x＝2时，y＝﹣5，当x＝﹣2时，y＝5，
对于图象G1，在y轴右侧，当y＝5时，则5＝（x﹣2）2﹣5，
∴x＝2+＞3，
对于图象G2，在y轴左侧，当y＝﹣5时，则﹣5＝﹣（x+2）2+5，
∴x＝﹣2﹣，
∵当k≤x≤3（k＜3）时，图象G对应函数的最大值为5，最小值为﹣5，
∴﹣2﹣≤k≤﹣2；
（3）如图2，
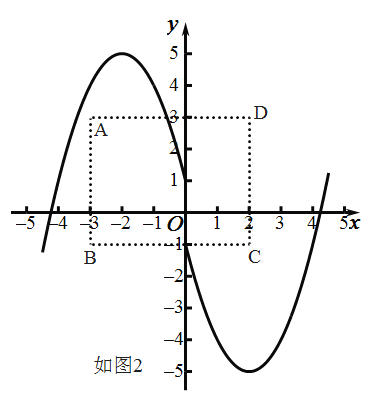
∵图象G2的解析式为：y＝﹣（x+2）2+4﹣n，图象G1的解析式为：y＝（x﹣2）2+n﹣4，
∴图象G2的顶点坐标为（﹣2，﹣n+4），与y轴交点为（0，﹣n），图象G1的顶点坐标为（2，n﹣4），与y轴交点为（0，n），
当n≤﹣1时，图象G1与矩形ABCD最多1个交点，图象G2与矩形ABCD最多1交点，
当﹣1＜n＜0时，图象G1与矩形ABCD有1个交点，图象G2与矩形ABCD有3交点，
当n＝0时，图象G1与矩形ABCD有1个交点，图象G2与矩形ABCD有2交点，共三个交点，
当0＜n≤1时，图象G1与矩形ABCD有1个交点，图象G2与矩形ABCD有1交点，
当1＜n＜3时，图象G1与矩形ABCD有1个交点，图象G2与矩形ABCD有2交点，共三个交点，
当3≤n＜7时，图象G1与矩形ABCD有2个交点，当3≤n＜5时，图象G2与矩形ABCD有2个交点，n＝5时，图象G2与矩形ABCD有1个交点，n＞5时，没有交点，
∵矩形ABCD的边与图象G有且只有三个公共点，
∴n＝5，
当n≥7时，图象G1与矩形ABCD最多1个交点，图象G2与矩形ABCD没有交点，
综上所述：当n＝0，n＝5，1＜n＜3时，矩形ABCD的边与图象G有且只有三个公共点．
