题目内容
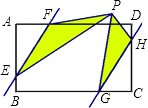
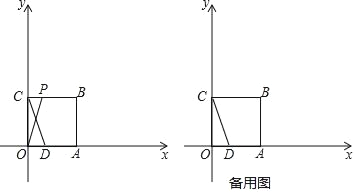
【题目】如图,在平面直角坐标系中,O是坐标原点,正方形OABC的顶点A、C分别在x轴与y轴上,已知正方形边长为3,点D为x轴上一点,其坐标为(1,0),连接CD,点P从点C出发以每秒1个单位的速度沿折线C→B→A的方向向终点A运动,当点P与点A重合时停止运动,运动时间为t秒.
(1)连接OP,当点P在线段BC上运动,且满足△CPO≌△ODC时,求直线OP的表达式;
(2)连接PC,求△CPD的面积S关于t的函数表达式;
(3)点P在运动过程中,是否存在某个位置使得△CDP为等腰三角形,若存在,直接写出点P的坐标,若不存在,说明理由.
【答案】(1)y=3x;(2)S=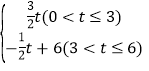 ;(3)满足条件的点P坐标为(2,3)或(3,
;(3)满足条件的点P坐标为(2,3)或(3,![]() )或(3,2)或(3,
)或(3,2)或(3,![]() ).
).
【解析】
(1) 四边形ABCO是正方形, 可得COD=∠OCP, OC=CO继而证明△CPO≌△ODC, 可得P点坐标,即可确定OP解析式;
(2) 分当点P在线段BC上时,当点P在线段AB上时两种情况讨论即可;
(3) 存在, 分别以DC=DP1, DC=DP2, CD=CP3, P4C=P4D四种情况考虑, 利用勾股定理及图形与坐标性质求出P坐标即可.
(1)∵四边形ABCO是正方形,
∴∠COD=∠OCP,∵OC=CO,
∴当CP=OD=1时,△CPO≌△ODC,
∴P(1,3),
设直线OP的解析式为y=kx,则有3=k,
∴直线OP的解析式为y=3x.
(2)当点P在线段BC上时,如图1中,
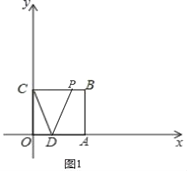
S=![]() CPCO=
CPCO=![]() t(0<t≤3),
t(0<t≤3),
当点P在线段AB上时,如图2中,
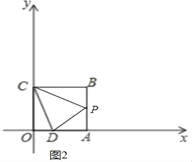
BP=t﹣3,AP=3﹣(t﹣3)=6﹣t,
S=3×3﹣![]() ×1×3﹣
×1×3﹣![]() ×3×(t﹣3)﹣
×3×(t﹣3)﹣![]() ×2×(6﹣t)=﹣
×2×(6﹣t)=﹣![]() t=6(3<t≤6),
t=6(3<t≤6),
综上所述,S=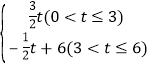 .
.
(3)如图3中,
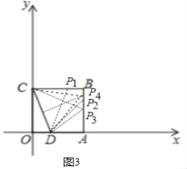
①当DC=DP1时,P1(2,3),
②当DC=DP2时,AP2=![]() =
=![]() ,
,
∴P2(3,![]() ).
).
③当CD=CP3=![]() 时,BP3=
时,BP3=![]() =1,
=1,
∴P3(3,2).
④当P4C=P4D时,设AP4=a,
则有22+a2=32+(3﹣a)2,
解得a=![]() ,
,
∴P4(3,![]() ),
),
综上所述,满足条件的点P坐标为(2,3)或(3,![]() )或(3,2)或(3,
)或(3,2)或(3,![]() ).
).