题目内容
【题目】计算下面各题
（1）计算：﹣22+ 
﹣2cos60°+|﹣3|；
（2）解不等式组：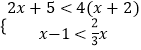 
．
【答案】
（1）解：﹣22+（ 
）﹣1﹣2cos60°+|﹣3|，
=﹣4+3﹣2× 
+3，
=﹣4+3﹣1+3，
=﹣5+6，
=1；
（2）解：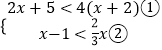 
解不等式①，得2x+5＜4x+8，
解得x＞﹣ 
，
解不等式②，得3x﹣3＜2x，
解得x＜3，
所以，原不等式组的解集是﹣ ＜x＜3
【解析】（1）根据有理数的乘方运算，有理数的负整数指数次幂等于正整数指数次幂的倒数，60°角的余弦值等于 ，绝对的性质计算即可得解；（2）先求出两个不等式的解集，再求其公共解．
【考点精析】本题主要考查了整数指数幂的运算性质和一元一次不等式组的解法的相关知识点，需要掌握aman=am+n(m、n是正整数)；（am）n=amn(m、n是正整数)；(ab)n=anbn(n是正整数)；am/an=am-n(a不等于0，m、n为正整数）；（a/b）n=an/bn(n为正整数)；解法：①分别求出这个不等式组中各个不等式的解集；②利用数轴表示出各个不等式的解集；③找出公共部分；④用不等式表示出这个不等式组的解集．如果这些不等式的解集的没有公共部分，则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )才能正确解答此题．
应用题作业本系列答案
暑假作业暑假快乐练西安出版社系列答案
【题目】随着信息技术的快速发展，“互联网+”渗透到我们日常生活的各个领域，网上在线学习交流已不再是梦，现有某教学网站策划了A，B两种上网学习的月收费方式：
收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/（元/min） |
A | 7 | 25 | 0.01 |
B | m | n | 0.01 |
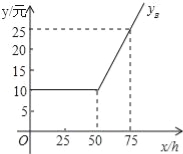
设每月上网学习时间为x小时，方案A，B的收费金额分别为yA，yB．
（1）如图是yB与x之间函数关系的图象，请根据图象填空：m= ；n=
（2）写出yA与x之间的函数关系式．
（3）选择哪种方式上网学习合算，为什么？
