题目内容
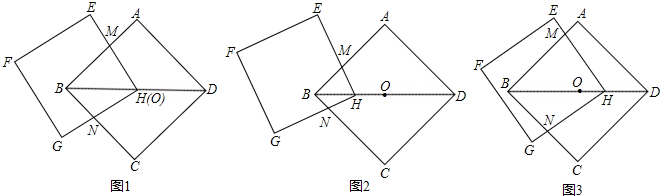
如图1,正方形ABCD是边长为1的正方形,正方形EFGH的边HE、HG与正方形ABCD的边AB、BC交于点M、N,顶点H在对角线BD上移动,设点M、N到BD的距离分别是hM、hN,四边形MBNH的面积是S.
(1)当顶点H和正方形ABCD的中心O重合时(图1),S=
,hM+hN=
(只要求写出结果,不用证明);
(2)若顶点H为OB的中点(图2),S=
,hM+hN=
(只要求写出结果,不用证明);
(3)按要求完成下列问题:
我们准备探索:当BH=n时,S=
n2
n2,hM+hN=
①简要写出你的探索过程;②在上面的横线上填上你的结论;③证明你得到的结论.
(1)当顶点H和正方形ABCD的中心O重合时(图1),S=
| 1 |
| 4 |
| 1 |
| 4 |
| ||
| 2 |
| ||
| 2 |
(2)若顶点H为OB的中点(图2),S=
| 1 |
| 16 |
| 1 |
| 16 |
| ||
| 4 |
| ||
| 4 |
(3)按要求完成下列问题:
我们准备探索:当BH=n时,S=
| 1 |
| 2 |
| 1 |
| 2 |
n
n
;①简要写出你的探索过程;②在上面的横线上填上你的结论;③证明你得到的结论.

分析:(1)当顶点H和正方形ABCD的中心O重合时,BH=
BD,H点分别作AB、BC的垂线HI和HJ,垂足分别为I、J.先由正方形的性质得出BD平分∠ABC,∠ABC=90°,由角平分线的性质得到HI=HJ,垂线的定义得到∠HIB=∠HJB=90°,根据一组邻边相等的矩形是正方形证明四边形IBJH是正方形,再利用ASA证明△HMI≌△HNJ,则S四边形MBNH=S正方形HIBJ,根据正方形的面积公式求出S=
BH2=
;又S四边形MBNH=S△HMB+S△HNB=
BH(hM+hN),将数据代入即可求出hM+hN=
;
(2)当顶点H为OB的中点时,BH=
BD,同(1)可求出S=
BH2=
;hM+hN=
;
(3)当BH=n时,同(1)可求出S=
BH2=
n2;hM+hN=n.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| ||
| 2 |
(2)当顶点H为OB的中点时,BH=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 16 |
| ||
| 4 |
(3)当BH=n时,同(1)可求出S=
| 1 |
| 2 |
| 1 |
| 2 |
解答: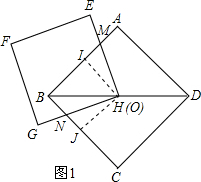 解:(1)当顶点H和正方形ABCD的中心O重合时,如图1,
解:(1)当顶点H和正方形ABCD的中心O重合时,如图1,
过H点分别作AB、BC的垂线HI和HJ,垂足分别为I、J.
∵四边形ABCD是正方形,
∴BD平分∠ABC,∠ABC=90°,
∵HI⊥AB于I,HJ⊥BC于J,
∴HI=HJ,∠HIB=∠HJB=90°,
∴四边形IBJH是正方形.
在△HMI和△HNJ中,
,
∴△HMI≌△HNJ,
∴S△HMI=S△HNJ,
∴S四边形MBNH=S△HMB+S△HNB=S△HMI+S△HBI+S△BHJ-S△HNJ=S△HBI+S△BHJ=S正方形HIBJ=
BH2=
(
BD)2=
×(
)2=
;
又∵S四边形MBNH=S△HMB+S△HNB=
BH•hM+
BH•hN=
BH(hM+hN),
∴
=
×
(hM+hN),
∴hM+hN=
;
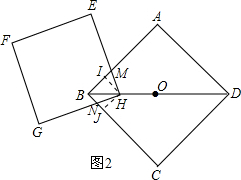 (2)当顶点H为OB的中点时,如图2,
(2)当顶点H为OB的中点时,如图2,
过H点分别作AB、BC的垂线HI和HJ,垂足分别为I、J.
同(1)可证,四边形IBJH是正方形且△HMI≌△HNJ,
∴S△HMI=S△HNJ,
∴S四边形MBNH=S正方形HIBJ=
BH2=
(
BD)2=
×(
)2=
;
又∵S四边形MBNH=S△HMB+S△HNB=
BH•hM+
BH•hN=
BH(hM+hN),
∴
=
×
(hM+hN),
∴hM+hN=
;
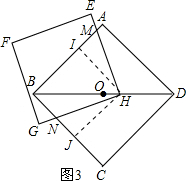 (3)当BH=n时,如图3,
(3)当BH=n时,如图3,
过H点分别作AB、BC的垂线HI和HJ,垂足分别为I、J.
同(1)可证,四边形IBJH是正方形且△HMI≌△HNJ,
∴S△HMI=S△HNJ,
∴S四边形MBNH=S正方形HIBJ=
BH2=
n2;
又∵S四边形MBNH=S△HMB+S△HNB=
BH•hM+
BH•hN=
BH(hM+hN),
∴
n2=
n(hM+hN),
∴hM+hN=n.
故答案为:(1)
,
;(2)
,
;(3)
n2,n.
 解:(1)当顶点H和正方形ABCD的中心O重合时,如图1,
解:(1)当顶点H和正方形ABCD的中心O重合时,如图1,过H点分别作AB、BC的垂线HI和HJ,垂足分别为I、J.
∵四边形ABCD是正方形,
∴BD平分∠ABC,∠ABC=90°,
∵HI⊥AB于I,HJ⊥BC于J,
∴HI=HJ,∠HIB=∠HJB=90°,
∴四边形IBJH是正方形.
在△HMI和△HNJ中,
|
∴△HMI≌△HNJ,
∴S△HMI=S△HNJ,
∴S四边形MBNH=S△HMB+S△HNB=S△HMI+S△HBI+S△BHJ-S△HNJ=S△HBI+S△BHJ=S正方形HIBJ=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 4 |
又∵S四边形MBNH=S△HMB+S△HNB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 4 |
| 1 |
| 2 |
| ||
| 2 |
∴hM+hN=
| ||
| 2 |
 (2)当顶点H为OB的中点时,如图2,
(2)当顶点H为OB的中点时,如图2,过H点分别作AB、BC的垂线HI和HJ,垂足分别为I、J.
同(1)可证,四边形IBJH是正方形且△HMI≌△HNJ,
∴S△HMI=S△HNJ,
∴S四边形MBNH=S正方形HIBJ=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| ||
| 4 |
| 1 |
| 16 |
又∵S四边形MBNH=S△HMB+S△HNB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 16 |
| 1 |
| 2 |
| ||
| 4 |
∴hM+hN=
| ||
| 4 |
 (3)当BH=n时,如图3,
(3)当BH=n时,如图3,过H点分别作AB、BC的垂线HI和HJ,垂足分别为I、J.
同(1)可证,四边形IBJH是正方形且△HMI≌△HNJ,
∴S△HMI=S△HNJ,
∴S四边形MBNH=S正方形HIBJ=
| 1 |
| 2 |
| 1 |
| 2 |
又∵S四边形MBNH=S△HMB+S△HNB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴hM+hN=n.
故答案为:(1)
| 1 |
| 4 |
| ||
| 2 |
| 1 |
| 16 |
| ||
| 4 |
| 1 |
| 2 |
点评:本题考查了正方形的判定与性质,角平分线的性质,全等三角形的判定与性质,三角形、四边形的面积,综合性较强,难度一般,体现了由特殊到一般的思想.

练习册系列答案
相关题目
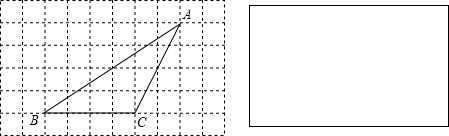
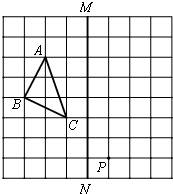 21、如图,在正方形网格上的一个△ABC.(其中点A、B、C均在网格上)
21、如图,在正方形网格上的一个△ABC.(其中点A、B、C均在网格上)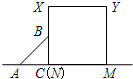 (2012•安庆一模)如图,等腰直角△ABC沿MN所在的直线以2cm/min的速度向右作匀速运动.如果MN=2AC=4cm,那么△ABC和正方形XYMN重叠部分的面积S(cm2)与匀速运动所用时间t(min)之间的函数的大致图象是( )
(2012•安庆一模)如图,等腰直角△ABC沿MN所在的直线以2cm/min的速度向右作匀速运动.如果MN=2AC=4cm,那么△ABC和正方形XYMN重叠部分的面积S(cm2)与匀速运动所用时间t(min)之间的函数的大致图象是( )
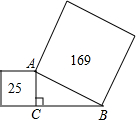 如图,以Rt△ABC的斜边和一直角边为边长向外作正方形,面积分别为169和25,则另一直角边的长度BC为( )
如图,以Rt△ABC的斜边和一直角边为边长向外作正方形,面积分别为169和25,则另一直角边的长度BC为( )