题目内容
 (2012•安庆一模)如图,等腰直角△ABC沿MN所在的直线以2cm/min的速度向右作匀速运动.如果MN=2AC=4cm,那么△ABC和正方形XYMN重叠部分的面积S(cm2)与匀速运动所用时间t(min)之间的函数的大致图象是( )
(2012•安庆一模)如图,等腰直角△ABC沿MN所在的直线以2cm/min的速度向右作匀速运动.如果MN=2AC=4cm,那么△ABC和正方形XYMN重叠部分的面积S(cm2)与匀速运动所用时间t(min)之间的函数的大致图象是( )分析:分t<1时,重叠部分是梯形,表示出AN,然后根据梯形等腰直角三角形的性质求出梯形的上底,再利用梯形的面积公式列式整理即可;
1≤t≤2时,重叠部分是△ABC,根据三角形的面积公式列式计算即可得解;
2≤t≤3时,重叠部分是三角形,表示出AM的长度,然后根据等腰直角三角形的面积公式列式整理即可,最后根据相应的函数图象找出符合条件的选项即可.
1≤t≤2时,重叠部分是△ABC,根据三角形的面积公式列式计算即可得解;
2≤t≤3时,重叠部分是三角形,表示出AM的长度,然后根据等腰直角三角形的面积公式列式整理即可,最后根据相应的函数图象找出符合条件的选项即可.
解答: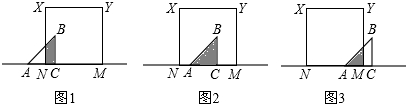 解:∵△ABC的运动速度是2cm/min,MN=2AC=4cm,
解:∵△ABC的运动速度是2cm/min,MN=2AC=4cm,
∴2÷2=1min,
4÷2=2min,
(4+2)÷2=3min,
如图1,当t<1时,重叠部分为梯形,面积y=
(2-2t+2)×t=-t2+2t=-(t-1)2+1,
如图2,当1≤t≤2时,重叠部分为△ABC,面积y=
×2×2=2,
如图3,当2≤t≤3时,重叠部分是三角形,面积y=
[2-(2t-4)][2-(2t-4)]=2(t-3)2,
图象为两段二次函数图象,中间是一条线段.
纵观各选项,只有D选项符合.
故选D.
 解:∵△ABC的运动速度是2cm/min,MN=2AC=4cm,
解:∵△ABC的运动速度是2cm/min,MN=2AC=4cm,∴2÷2=1min,
4÷2=2min,
(4+2)÷2=3min,
如图1,当t<1时,重叠部分为梯形,面积y=
| 1 |
| 2 |
如图2,当1≤t≤2时,重叠部分为△ABC,面积y=
| 1 |
| 2 |
如图3,当2≤t≤3时,重叠部分是三角形,面积y=
| 1 |
| 2 |
图象为两段二次函数图象,中间是一条线段.
纵观各选项,只有D选项符合.
故选D.
点评:本题考查了动点问题的函数图象,判断出重叠部分的形状并求出相应的函数关系式是解题的关键.

练习册系列答案
相关题目
 (2012•安庆一模)如图,在3×3的网格中,每个网格线的交点称为格点.已知图中A、B两个格点,请在图中再寻找另一个格点C,使△ABC成为等腰三角形,则满足条件的点C有( )
(2012•安庆一模)如图,在3×3的网格中,每个网格线的交点称为格点.已知图中A、B两个格点,请在图中再寻找另一个格点C,使△ABC成为等腰三角形,则满足条件的点C有( ) (2012•安庆一模)如图,在?ABCD中,点E是边AB的中点,连接DE交对角线AC于点O,则△AOE与△COD的面积比为
(2012•安庆一模)如图,在?ABCD中,点E是边AB的中点,连接DE交对角线AC于点O,则△AOE与△COD的面积比为 (2012•安庆一模)如图,直线l1∥l2,∠1=40°,∠2=65°,则∠3=( )
(2012•安庆一模)如图,直线l1∥l2,∠1=40°,∠2=65°,则∠3=( )
 (2012•安庆一模)地面上有一棵高为6m的大树,早晨8:00太阳光与地面的夹角为30°,此时这棵大树在水平地面上的影子长为
(2012•安庆一模)地面上有一棵高为6m的大树,早晨8:00太阳光与地面的夹角为30°,此时这棵大树在水平地面上的影子长为