题目内容
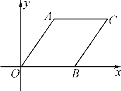
【题目】如图,A,B,C三点在同一直线上,分别以AB,BC(AB>BC)为边,在直线AC的同侧作等边ΔABD和等边ΔBCE,连接AE交BD于点M,连接CD交BE于点N,连接MN. 以下结论:①AE=DC,②MN//AB,③BD⊥AE,④∠DPM=60°,⑤ΔBMN是等边三角形.其中正确的是__________(把所有正确的序号都填上).

【答案】①②④⑤
【解析】
①由三角形ABD与三角形BCE都为等边三角形,利用等边三角形的性质得到两条边对应相等,两个角相等都为60°,利用SAS即可得到三角形ABE与三角形DBC全等即可得结论;
②由①中三角形ABE与三角形DBC全等,利用全等三角形的对应角相等得到一对角相等,再由∠ABD=∠EBC=60°,利用平角的定义得到∠MBE=∠NBC=60°,再由EB=CB,利用ASA可得出三角形EMB与三角形CNB全等,利用全等三角形的对应边相等得到MB=NB,再由∠MBE=60°,利用有一个角为60°的等腰三角形为等边三角形可得出三角形BMN为等边三角形;可得∠BMN=60°,进行可得∠BMN=∠ABD,故MN//AB,从而可判断②,⑤正确;
③无法证明PM=PN,因此不能得到BD⊥AE;
④由①得∠EAB=∠CDB,根据三角形内角和和外角的性质可证得结论.
①∵等边△ABD和等边△BCE,
∴AB=DB,BE=BC,∠ABD=∠EBC=60°,
∴∠ABE=∠DBC=120°,
在△ABE和△DBC中,
∵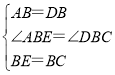 ,
,
∴△ABE≌△DBC(SAS),
∴AE=DC,
故①正确;
∵△ABE≌△DBC,
∴∠AEB=∠DCB,
又∠ABD=∠EBC=60°,
∴∠MBE=180°-60°-60°=60°,
即∠MBE=∠NBC=60°,
在△MBE和△NBC中,
∵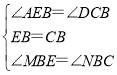 ,
,
∴△MBE≌△NBC(ASA),
∴BM=BN,∠MBE=60°,
则△BMN为等边三角形,
故⑤正确;
∵△BMN为等边三角形,
∴∠BMN=60°,
∵∠ABD=60°,
∴∠BMN=∠ABD,
∴MN//AB,
故②正确;
③无法证明PM=PN,因此不能得到BD⊥AE;
④由①得∠EAB=∠CDB,∠APC+∠PAC+∠PCA=180°,
∴∠PAC+∠PCA=∠PDB+∠PCB=∠DBA=60°,
∵∠DPM =∠PAC+∠PCA
∴∠DPM =60°,故④正确,
故答案为:①②④⑤.