题目内容
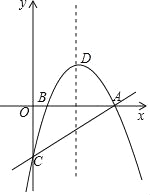
【题目】在平面直角坐标系xOy中,抛物线![]() 经过点A(-3,4).
经过点A(-3,4).
(1)求b的值;
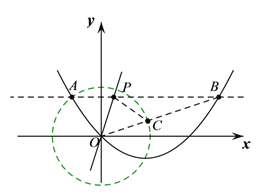
(2)过点A作![]() 轴的平行线交抛物线于另一点B,在直线AB上任取一点P,作点A关于直线OP的对称点C;
轴的平行线交抛物线于另一点B,在直线AB上任取一点P,作点A关于直线OP的对称点C;
①当点C恰巧落在![]() 轴时,求直线OP的表达式;
轴时,求直线OP的表达式;
②连结BC,求BC的最小值.
【答案】(1)-3;(2)①OP的表达式为![]() 或
或![]() ,②BC的最小值为
,②BC的最小值为![]() .
.
【解析】试题分析:(1)把点A坐标代入解析式即可得;
(2)①由对称性可知OA=OC,AP=CP,由AP∥OC,可得∠1=∠2,再根据轴对称可得∠AOP=∠2,从而得∠AOP=∠1,得到AP=AO,再根据A点坐标即可得AP的长,从而得P点的坐标,利用待定系数法即可得解析式;
②以O为圆心,OA长为半径作⊙O,连接BO,交⊙O于点C,此时BC的值最小.
试题解析:(1)∵抛物线![]() 经过点A(-3,4),
经过点A(-3,4),
令x=-3,代入![]() ,则
,则![]() ,
,
∴b=-3;
(2)①由对称性可知OA=OC,AP=CP,
∵AP∥OC,∴∠1=∠2,
又∵∠AOP=∠2,∴∠AOP=∠1,
∴AP=AO,
∵A(-3,4),
∴AO=5,∴AP=5,
∴P1(2,4),
同理可得P2(-8,4),
∴OP的表达式为![]() 或
或![]() ;
;
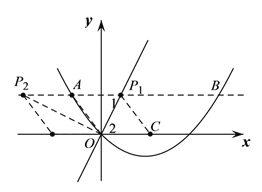
②以O为圆心,OA长为半径作⊙O,连接BO,交⊙O于点C,此时BC值最小,
把y=4代入![]() ,解得:x1=12,x2=-3,∴B(12,4),
,解得:x1=12,x2=-3,∴B(12,4),
∴OB=![]() , ∴BC的最小值为
, ∴BC的最小值为![]() .
.

练习册系列答案
相关题目