题目内容
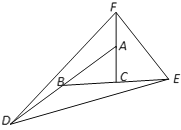
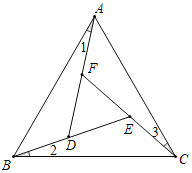
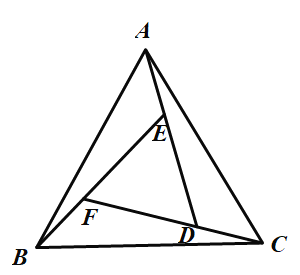
【题目】如图，在等边△ABC中，过A，B，C三点在三角形内分别作∠1＝∠2＝∠3，三个角的边相交于D，E，F，
（1）你认为△DEF是什么三角形？并证明你的结论；
（2）当∠1，∠2，∠3三个角同时逐渐增大仍保持相等时，△DEF会发生什么变化？试说明理由．
【答案】（1）△DEF是等边三角形，见解析；（2）△DEF先变小，再变为一点，再逐渐变大；见解析
【解析】
（1）利用ASA证明△ABD≌△BCE,△BCE≌△CAF，得出∠ADB＝∠BEC＝∠CFA，证出∠FDE＝∠DEF＝∠EFD，即可得出△DEF是等边三角形；
（2）通过分析等边三角形的边长即可得出它的变化情况，分三种情况：当
时，△DEF逐渐变小；当∠1＝30°时，△DEF变为一点；当
，△DEF逐渐变大．
解：（1）△DEF是等边三角形，理由如下：
∵△ABC是等边三角形，
∴AB＝BC＝CA，∠BAC＝∠CBA＝∠ACB＝60°，
∵∠1＝∠2＝∠3，
∴∠ABD＝∠BCE＝∠CAF，
在△ABD和△BCE中，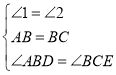
，
∴△ABD≌△BCE（ASA），
∴∠ADB＝∠BEC，
在△BCE和△CAF中，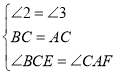
，
∴△BCE≌△CAF（ASA），
∴∠BEC＝∠CFA，
∴∠ADB＝∠BEC＝∠CFA，
∴∠FDE＝∠DEF＝∠EFD，
∴△DEF是等边三角形；
（2）△DEF先变小，再变为一点，再逐渐变大；理由如下：
当∠1，∠2，∠3三个角或时，△DEF均为等边三角形；
∵△ABD≌△BCE，△BCE≌△CAF
∴
当∠1，∠2，∠3三个角在范围内同时逐渐增大仍保持相等时，
BD,CE,EF逐渐增大，所以等边三角形的边长逐渐变小；
∴当时，△DEF逐渐变小；
当∠1＝30°时，△DEF变为一点；
由（1）可知△ABE≌△BCF，△BCF≌△ADC
∴
当∠1，∠2，∠3三个角在范围内同时逐渐增大仍保持相等时，
AE,BF,CD逐渐减小，所以等边三角形的边长逐渐变大；
∴当时，△DEF逐渐变大．
