题目内容
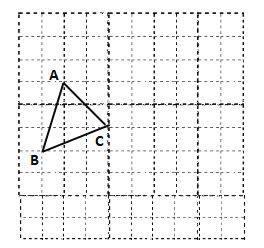
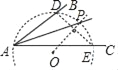
【题目】如图是由边长为![]() 的小正方形构成的网格,每个小正方形的顶点叫做格点,
的小正方形构成的网格,每个小正方形的顶点叫做格点,![]() 的顶点在格点.请选择适当的格点用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由.
的顶点在格点.请选择适当的格点用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由.
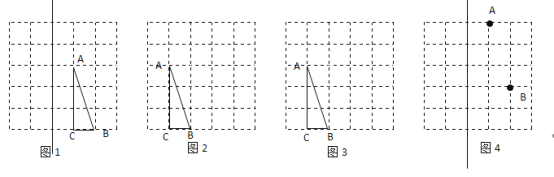
(1)如图![]() ,作
,作![]() 关于直线
关于直线![]() 的对称图形
的对称图形![]() ;
;
(2)如图![]() ,作
,作![]() 的高
的高![]() ;
;
(3)如图![]() ,作
,作![]() 的中线
的中线![]() ;
;
(4)如图![]() ,在直线
,在直线![]() 上作出一条长度为
上作出一条长度为![]() 个单位长度的线段
个单位长度的线段![]() 在
在![]() 的上方
的上方![]() ,使
,使![]() 的值最小.
的值最小.
【答案】(1)图见解析;(2)图见解析;(3)图见解析;(4)图见解析
【解析】
(1)分别找到A、B、C关于直线l的对称点![]() ,连接
,连接![]() 、
、![]() 、
、![]() 即可;
即可;
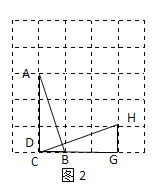
(2)如解图2,连接CH,交AB于点D,利用SAS证出△ACB≌△CGH,从而得出∠BAC=∠HCG,然后利用等量代换即可求出∠CDB=90°;
(3)如解图3,连接CP交AB于点E,利用矩形的性质可得AE=BE;
(4)如解图4,找出点A关于l的对称点A1,设点A1正下方的格点为C,连接CB,交直线l于点N,设点B正上方的格点为D,连接A1D,交直线l于点M,连接AM,根据平行四边形的性质和两点之间线段最短即可推出此时MN即为所求.
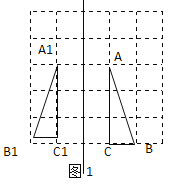
解:(1)分别找到A、B、C关于直线l的对称点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,如图1所示,
,如图1所示,![]() 即为所求;
即为所求;
(2)如图2所示连接CH,交AB于点D,
在△ACB和△CGH中
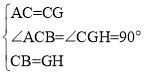
∴△ACB≌△CGH
∴∠BAC=∠HCG
∵∠BAC+∠ABC=90°
∴∠HCG+∠ABC=90°
∴∠CDB=90°
∴CD为△ABC的高,故CD即为所求;
(3)如图3所示,连接CP交AB于点E
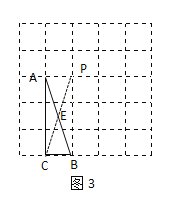
由图可知:四边形ACBP为矩形
∴AE=EB
∴CE为△ABC的中线,故CE即为所求;
(4)如图4所示,找出点A关于l的对称点A1,设点A1正下方的格点为C,连接CB,交直线l于点N,设点B正上方的格点为D,连接A1D,交直线l于点M,连接AM
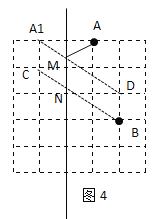
根据对称性可知:AM=A1M
由图可知:A1C=BD=1个单位长度,A1C∥BD∥直线l
∴四边形A1CBD为平行四边形
∴A1D∥BC
∴四边形A1CNM和四边形MNBD均为平行四边形
∴A1M=CN,MN=BD=1个单位长度
∴AM=CN
∴AM+NB=CN+NB=CB,
根据两点之间线段最短,此时AM+NB最小,而MN=1个单位长度为固定值,
∴此时![]() 最小,故此时MN即为所求.
最小,故此时MN即为所求.

 阅读快车系列答案
阅读快车系列答案