Question

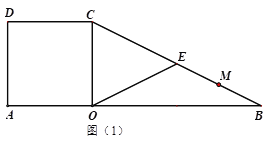
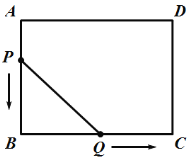
【题目】如图，在矩形中，，，点从点开始沿边向终点以的速度移动，与此同时，点从点开始沿边向终点以的速度移动．如果分别从同时出发，当点运动到点时，两点停止运动，设运动时间为秒．

（1）填空：__________，_________；（用含的代数式表示）

（2）当为何值时，的长度等于？

（3）当为何值时，五边形的面积有最小值？最小值为多少？

Answer 1

【答案】（1），；（2）当秒时，的长度等于；（3）当秒时，五边形的面积有最小值，最小值为39．

【解析】

（1）根据路程与速度的关系解决问题即可．

（2）利用勾股定理构建方程即可解决问题．

（3）利用分割法构建方程，转化为二次函数，即可解决问题．

解：（1）∵P从点A开始沿边AB向终点B以1cm/s的速度移动，

∴，

∵，

∴，

∵点Q从点B开始沿边BC向终点C以2cm/s的速度移动，

∴；

（2）由题意，由勾股定理，得：．

解得：（不合题意，舍去），．

∴当秒时，的长度等于．

（3）存在．

设五边形的面积为S.

∵，

∴

∴当秒时，五边形的面积有最小值，最小值为39．