题目内容

12．已知分式$\frac{x-3}{{x}^{2}-5x+a}$，当x=2时，分式无意义，则a=6；当a＜6时，使分式无意义的x的值共有2个．

分析 根据分母等于零分式无意义，可得答案．

解答 解：由题意，得
22-5×2+a=0，
解得a=6，
x2-5x+a=0，
△=25-4a＞0，
方程有两个实数解，
故答案为：2．

点评 本题考查的是分式有意义的条件，熟知分式有意义的条件是分母不等于零是解答此题的关键．

练习册系列答案
相关题目
2．计算
（1）-2+6÷（-2）×$\frac{1}{2}$                
（2）24-|-0.5|+（-3.2）-|-2$\frac{2}{5}$|-（-4.7）
（3）-23-|-3|+4÷（-$\frac{3}{8}$）×（-3）
（4）-0.252+（-0.5）3÷（$\frac{1}{8}$-$\frac{1}{2}$）×（-1）10．
3．如图1所示，在直角坐标系中，边长为12的等边△ABC的边BC在x轴上，BC边上的高AD在y轴上，点D与原点O重合，过D点作AB边的垂线，交AB边于点E，交AC的延长线于点M．
（1）求证：OC=MC；
（2）将等边△ABC整体沿x轴的正方向匀速平移，当点B到达原点O时，图形停止运动．若边AB与y轴交于点F，请思考并解决以下问题：
①如图2，延长CA交y轴于点G．如果△ABC平移的速度为每秒1个单位长度，当△AGF与△CDM全等时，平移了多长时间？
②在线段OC上取一点N，连接FN并延长交射线AC于点Q，是否存在一点N，使得CQ=FB？若存在，求线段ON的长；若不存在，说明理由．
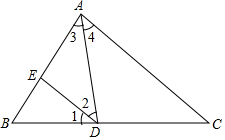20．如图，已知∠1=∠C，∠2=∠3，那么AD平分∠BAC，请你说明为什么．
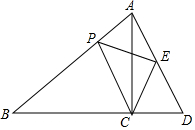7．开口向上的抛物线经过A（-1，0），B（3，0），过（0，-2）点的直线l与x轴平行，抛物线与直线l有交点，结合函数图象，求a的取值范围．
17．如图，△ABC是等腰直角三角形，P是斜边AB上的一点，以CP为斜边作等腰Rt△CPE，连接AE交BC所在直线于D．求证：AE=ED．
4．随着人们环保意识的不断增强，我市家庭电动自行车的拥有量逐年增加，据统计，某小区2011年底拥有家庭电动自行车250辆．2013年底家庭电动自行车的拥有量达列360辆．
（1）若该小区2011年底到2014年底家庭电动自行车的拥有量的年平均增长率相同，则该小区到2014年底电动自行车将达到多少辆？
（2）为了缓解停车难矛盾，该小区决定再新建10个停车位，据测算，建造费用分别为室内车位2000元/个，露天车位800元/个，考虑到实际因素，计划露天车位的数量至少5个，但不超过室内车位数量的2倍，求该小区建造停车位的最低费用是多少万元，并写出费用最低的建造方案．
1．同底数幂的除法公式am÷an=am-n（a≠0，m，n都是正整数，并且m＞n）中，如果m＜n可以得到负整指数幂；a-p=$\frac{1}{{a}^{p}}$（a≠0，p是正整数），即任何不等于0的数的-p次幂等于这个数的p次幂的倒数，请你根据负整指数幂的定义求解下题：
（$\frac{1}{2}$）-1+|-3|+（2-$\sqrt{3}$）0+（-1）
5．阅览室某一书架上原有图书20本，规定每天归还图书为正，借出图书为负，经过两天借阅情况如下：（-3，+1），（-1，+2），则该书架上现有图书19本．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网