题目内容
17. 如图,△ABC是等腰直角三角形,P是斜边AB上的一点,以CP为斜边作等腰Rt△CPE,连接AE交BC所在直线于D.求证:AE=ED.
如图,△ABC是等腰直角三角形,P是斜边AB上的一点,以CP为斜边作等腰Rt△CPE,连接AE交BC所在直线于D.求证:AE=ED.
分析 先过点E作EF⊥BD于点F,过点C作CG⊥AB于G,得到∠CGP=∠EFC=90°,再根据∠GPC=∠FCE,判定△GPC∽△FCE,得出CG=$\sqrt{2}$EF,最后根据△ACG是等腰直角三角形,得到AC=$\sqrt{2}$CG=2EF,即可得到E是AD的中点.
解答  解:如图所示,过点E作EF⊥BD于点F,过点C作CG⊥AB于G,则∠CGP=∠EFC=90°,
解:如图所示,过点E作EF⊥BD于点F,过点C作CG⊥AB于G,则∠CGP=∠EFC=90°,
∵△CPE,△ABC都是等腰直角三角形,
∴∠PCE=∠B=45°,
∴∠BCP+∠GPC=135°,∠BCP+∠FCE=135°,
∴∠GPC=∠FCE,
∴△GPC∽△FCE,
∴EF:CG=CE:PC=1:$\sqrt{2}$,
即CG=$\sqrt{2}$EF,
又∵△ACG是等腰直角三角形,
∴AC=$\sqrt{2}$CG=2EF,
∵EF∥AC,
∴$\frac{DE}{DA}$=$\frac{EF}{AC}$=$\frac{1}{2}$,
∴AE=ED.
点评 本题主要考查了相似三角形的判定与性质,等腰直角三角形的性质以及平行线分线段成比例定理的综合应用,解决问题的关键是作辅助线构造相似三角形,运用相似三角形的对应边成比例进行推导.解题时注意:平行于三角形一边的直线截其他两边,所得的对应线段成比例.

练习册系列答案
相关题目
 如图,△ABC中,AD⊥BC于D,若BD=AD,BF=AC.求证:∠FBD=∠CAD.
如图,△ABC中,AD⊥BC于D,若BD=AD,BF=AC.求证:∠FBD=∠CAD. 如图,∠CAB=45°,AB=3,△ABC的面积为3,E为BC上任意一点,连AE,将△ABE,△ACE分别延AB,AC翻折至△ABM,△ACN,连MN,则MN的最小值$\frac{6}{5}$$\sqrt{10}$.
如图,∠CAB=45°,AB=3,△ABC的面积为3,E为BC上任意一点,连AE,将△ABE,△ACE分别延AB,AC翻折至△ABM,△ACN,连MN,则MN的最小值$\frac{6}{5}$$\sqrt{10}$.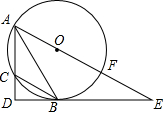 如图,已知△ABC是⊙O内接三角形,过点B作BD⊥AC于点D,连接AO并延长交⊙O于点F,交DB的延长线于点E,且点B是$\widehat{CF}$的中点.
如图,已知△ABC是⊙O内接三角形,过点B作BD⊥AC于点D,连接AO并延长交⊙O于点F,交DB的延长线于点E,且点B是$\widehat{CF}$的中点.