题目内容
7.开口向上的抛物线经过A(-1,0),B(3,0),过(0,-2)点的直线l与x轴平行,抛物线与直线l有交点,结合函数图象,求a的取值范围.分析 求得对称轴,如果过(0,-2)点的直线l与x轴平行,抛物线与直线l有交点,则开口向上,当顶点为(1,-2)时求得a的值,即可求得a的取值.
解答  解:∵物线经过A(-1,0),B(3,0),
解:∵物线经过A(-1,0),B(3,0),
∴对称轴x=$\frac{-1+3}{2}$=1,
当抛物线的顶点为(1,-2)时,则y=a(x-1)2-2,
代入(-1,0)得,4a-2=0,
解得a=$\frac{1}{2}$,
所以过(0,-2)点的直线l与x轴平行,抛物线与直线l有交点,则a的取值范围为a≥$\frac{1}{2}$.
点评 本题考查了二次函数图象上点的坐标特征,求得顶点为(1,-2)时的a的值是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
17.用科学记数法表示106 000,其中正确的是( )
| A. | 10.6×104 | B. | 10.6×106 | C. | 106×103 | D. | 1.06×105 |
2.扇形周长为1,当扇形的半径为R时,扇形有最大面积S,则R和S的值为( )
| A. | $\frac{1}{4}$,$\frac{1}{16}$ | B. | $\frac{1}{2}$,$\frac{1}{8}$ | C. | $\frac{1}{4}$,$\frac{1}{8}$ | D. | $\frac{1}{2}$,$\frac{1}{16}$ |
20.已知x=5是方程x-4+a=3的解,则a的值是( )
| A. | -1 | B. | 1 | C. | 2 | D. | -2 |
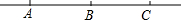 已知:A、B、C是一直线上顺次三点,并且BC=90.
已知:A、B、C是一直线上顺次三点,并且BC=90.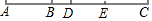 如图,已知线段AB=3cm,延长线段AB到C,使BC=2AB.
如图,已知线段AB=3cm,延长线段AB到C,使BC=2AB.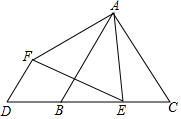 如图,点D在等边△ABC边CB的延长线上,点E是边BC上的动点,连结AE,在AE的左侧构造等边△AEF,连结DF,若DB=2,则DF的最小值是$\sqrt{3}$.
如图,点D在等边△ABC边CB的延长线上,点E是边BC上的动点,连结AE,在AE的左侧构造等边△AEF,连结DF,若DB=2,则DF的最小值是$\sqrt{3}$.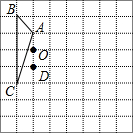 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求完成下列步骤:
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求完成下列步骤: