题目内容
3.如图1所示,在直角坐标系中,边长为12的等边△ABC的边BC在x轴上,BC边上的高AD在y轴上,点D与原点O重合,过D点作AB边的垂线,交AB边于点E,交AC的延长线于点M.(1)求证:OC=MC;
(2)将等边△ABC整体沿x轴的正方向匀速平移,当点B到达原点O时,图形停止运动.若边AB与y轴交于点F,请思考并解决以下问题:
①如图2,延长CA交y轴于点G.如果△ABC平移的速度为每秒1个单位长度,当△AGF与△CDM全等时,平移了多长时间?
②在线段OC上取一点N,连接FN并延长交射线AC于点Q,是否存在一点N,使得CQ=FB?若存在,求线段ON的长;若不存在,说明理由.
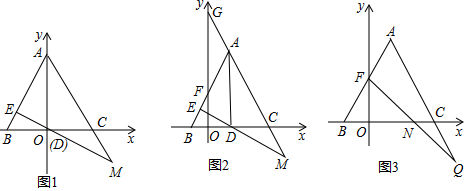
分析 (1)利用等边三角形的性质得:∠BAC=∠ABC=60°,再利用直角三角形的两锐角互余得:∠AME=∠COM=30°,所以OC=MC;
(2)①如图2,设平移t秒时,△AGF≌△CDM,先表示OC的长为6+t,根据30°角所对的直角边是斜边的一半列式可求得t的值;
②如图3,过Q作QH⊥x轴于H,则∠CHQ=90°,证明△BOF≌△CHQ和△FON≌△QHN,得ON=NH、OB=CH,根据等量代换可得结论.
解答 证明:(1)如图1,∵△ABC是等边三角形,
∴∠BAC=∠ABC=60°,
∵EM⊥AB,
∴∠AEM=∠BEO=90°,
∴∠AME=90°-60°=30°,∠EOB=90°-60°=30°,
∴∠AME=∠EOB,
∵∠EOB=∠COM,
∴∠AME=∠COM,
∴OC=MC;
(2)①设平移t秒时,△AGF≌△CDM,
则OD=t,
∵△ABC是等边三角形,AC=BC=12,
∵AD⊥BC,
∴CD=6,
∴AG=CD=6,
在Rt△OGC中,∵∠GCO=60°,
∴∠OGC=30°,
∴CG=2OC,
∴6+12=2(6+t),
t=3;
答:当△AGF与△CDM全等时,平移了3秒;
②如图3,过Q作QH⊥x轴于H,则∠CHQ=90°,
∵∠QCH=∠ACB=60°,∠ABC=60°,
∴∠ABC=∠QCH,
∵BF=CQ,∠BOF=∠CHQ=90°,
∴△BOF≌△CHQ,
∴FO=HQ,OB=CH,
∵∠FNO=∠QNH,∠FON=∠NHQ=90°,
∴△FON≌△QHN,
∴ON=NH,
∴ON+NH=ON+NC+CH=ON+NC+OB=BC=12,
∴ON=$\frac{1}{2}$BC=6.
点评 本题是三角形的综合题,考查了等边三角形、全等三角形的性质和判定及坐标与图形特点,要熟练掌握全等三角形的判定,要准确判断出所要证明的边或角相等是哪两个三角形全等所得;还利用作辅助线,构建两三角形全等也是本题的关键.

| A. | 3a+4b元 | B. | (3a+4b)元 | C. | (a+2b)元 | D. | (2a+6b)元 |
 如图,两只蚂蚁以相同的速度沿两条不同的路径,同时从A出发爬到B,则( )
如图,两只蚂蚁以相同的速度沿两条不同的路径,同时从A出发爬到B,则( )| A. | 乙比甲先到 | B. | 甲比乙先到 | C. | 甲和乙同时到 | D. | 无法确定 |
 已知:A、B、C是一直线上顺次三点,并且BC=90.
已知:A、B、C是一直线上顺次三点,并且BC=90. 如图,△ABC中,AD⊥BC于D,若BD=AD,BF=AC.求证:∠FBD=∠CAD.
如图,△ABC中,AD⊥BC于D,若BD=AD,BF=AC.求证:∠FBD=∠CAD. 如图,已知线段AB=3cm,延长线段AB到C,使BC=2AB.
如图,已知线段AB=3cm,延长线段AB到C,使BC=2AB.