Question

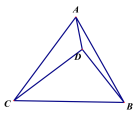
【题目】如图D为等边△ABC内一点，如果DA=3，DB=4，DC=5，那么△ABC的面积为______________．

Answer 1

【答案】

【解析】

此题根据旋转知识点分别绕点A逆时针旋转△ADC得到△AEB，分别根据旋转得到△ADE为等边三角形，△BDE为直角三角形，根据此求出面积，同理绕点C逆时针旋转△BDC得到△AFC，绕点B逆时针旋转△ADB得到△CMB，分别求出，，再根据求出△ABD的面积为．

如图：绕点A逆时针旋转△ADC得到△AEB，绕点C逆时针旋转△BDC得到△AFC，绕点B逆时针旋转△ADB得到△CMB，

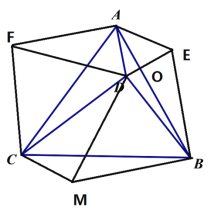
∵绕点A逆时针旋转△ADC得到△AEB，

∴AD=AE，∠DAE=∠CAB=60°，

∴△ADE为等边三角形，

即AD=AE=DE=3，

∴ ，

∴，

由旋转知：BE=DC=5，

又BD=4,

∴ ,

即△BDE为直角三角形，∠EDB=90°，

∴ ，

∴ ，

同理：，

，

由图知：，

∴，

，

，

即△ABD的面积为，

故答案为：．