题目内容
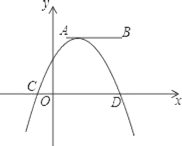
【题目】如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x+m)2+n的顶点在线段AB上,与x轴交于C,D两点(C在D的左侧),点C的横坐标最小值为﹣3,则点D的横坐标的最大值为_____.
【答案】8
【解析】
当C点横坐标最小时,抛物线顶点必为A(1,4),根据此时抛物线的对称轴,可判断出CD间的距离;当D点横坐标最大时,抛物线顶点为B(4,4),再根据此时抛物线的对称轴及CD的长,可判断出D点横坐标最大值.
解:当点C横坐标最小值为﹣3时,抛物线顶点为A(1,4),对称轴为直线x=1,此时D点横坐标为5,则CD=8;
当抛物线顶点为B(4,4)时,此时D点横坐标最大,抛物线对称轴为x=4,且CD=8,故C(0,0),D(8,0);
所以点D的横坐标最大值为8,
故答案为:8.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目