题目内容
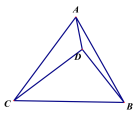
【题目】已知如图:在⊙O中,直径AB⊥弦CD于G,E为DC延长线上一点,BE交⊙O于点F.
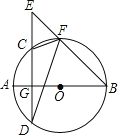
(1)求证:∠EFC=∠BFD;
(2)若F为半圆弧AB的中点,且2BF=3EF,求tan∠EFC的值.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接BD,圆心角、弧、弦间的关系得到∠BFD=∠CDB;根据邻补角的定义和园内接四边形对角互补的性质推知∠EFC=∠CDB,则∠EFC=∠BFD;
(2)如图,连OF,OC,BC,由于∠EFC所在的三角形不是直角三角形,欲求求正切值,需要将其转化为求∠BCG的正切值,据此推知相关线段的长度即可.
(1)证明:如图,连接BD,
∵AB⊥CD 且AB为直径,
∴弧CB=弧BD.
∴∠BFD=∠CDB.
又∵∠EFC+∠CFB=180°,
而∠CFB+∠CDB=180°,
∴∠EFC=∠CDB,
∴∠EFC=∠BFD;
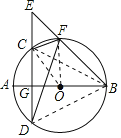
(2)解:如图,连OF,OC,BC,
∵弧CB=弧BD,
∴∠DCB=∠CDB,
∵∠EFC=∠CDB,
∴∠EFC=∠BFD=∠BCG,
又F为半圆AB的中点,
∴∠FOB=∠FOA=90°,
∴OF//CD,
∴OG:OB=EF:FB=2:3.
设OG=2x,则OB=OC=3x,则CG=![]() x,
x,
∴tan∠EFC=tan∠BCG=![]() =
=![]() .
.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目