题目内容
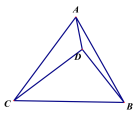
【题目】下面是小明设计的“在已知三角形的一边上取一点,使得这点到这个三角形的另外两边的距离相等”的尺规作图过程:
已知:△ABC.
求作:点D,使得点D在BC边上,且到AB,AC边的距离相等.
作法:如图,
作∠BAC的平分线,交BC于点D.则点D即为所求.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形 (保留作图痕迹);
(2)完成下面的证明.
证明:作DE⊥AB于点E,作DF⊥AC于点F,
∵AD平分∠BAC,
∴ = ( ) (填推理的依据) .
【答案】(1)详见解析;(2)DE,DF,角平分线上的点到角两边的距离相等.
【解析】
(1)根据尺规作图——角平分线的做法画图即可得到答案;
(2)根据角平分线上的点到角两边的距离相等即可得到答案;
解:(1)作∠BAC的角平分线,如图:
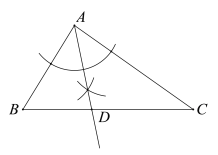
(2)作DE⊥AB于点E,作DF⊥AC于点F,
∵AD平分∠BAC,
∴DE=DF(角平分线上的点到角两边的距离相等).
故答案为:DE,DF,角平分线上的点到角两边的距离相等.

练习册系列答案
相关题目
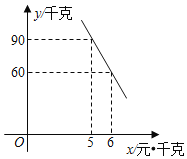
【题目】现在,步行运动深受广大健身爱好者的喜爱. 通过“微信运动”可以查询微信好友当天的行走步数.实验中学张老师根据该校![]() 名教师某日“微信运动”中的行走步数,绘制成如下两张统计表(不完整).
名教师某日“微信运动”中的行走步数,绘制成如下两张统计表(不完整).
步数 | 频数 | 频率 |
|
| 0.2 |
| 19 | 0.38 |
|
| 0.3 |
| 4 |
|
| 2 | 0.04 |
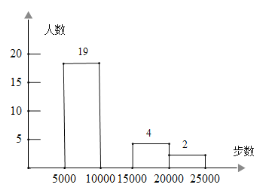
(1)写出左表中![]() 、
、![]() 、
、![]() 的值,并补全条形统计图;
的值,并补全条形统计图;
(2)实验中学所在的某县有![]() 名教师,用张老师调查的样本数据估计该县当天行走步数不少于
名教师,用张老师调查的样本数据估计该县当天行走步数不少于![]() 步的教师有多少人?
步的教师有多少人?
(3)在该校![]() 名教师中,随机选取当天行走步数不少于
名教师中,随机选取当天行走步数不少于![]() 步的
步的![]() 名教师参加“我运动,我健康”的征文活动,求选中的
名教师参加“我运动,我健康”的征文活动,求选中的![]() 名教师的行走步数都不小于
名教师的行走步数都不小于![]() 步的概率.
步的概率.