题目内容
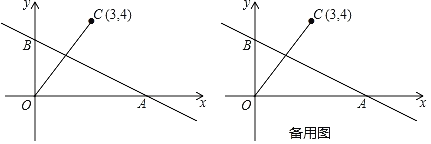
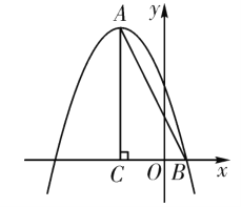
【题目】如图,在平面直角坐标系中,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点.
两点.
(1)求抛物线的解析式;
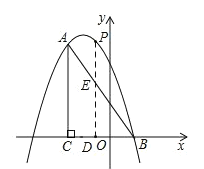
(2)点![]() 是直线
是直线![]() 上方抛物线上的一点,过点
上方抛物线上的一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交线段
,交线段![]() 于点
于点![]() ,使
,使![]() .
.
①求点![]() 的坐标和
的坐标和![]() 的面积;
的面积;
②在直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为直角三角形?若存在,直接写出符合条件的所有点
为直角三角形?若存在,直接写出符合条件的所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ,3;②存在,点
,3;②存在,点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
(1)先求出点C的坐标,再结合锐角三角函数求出AC的长度,进而得出点A的坐标,将点A和点B代入函数解析式即可得出答案;
(2)①先求出直线AB的解析式,设![]() ,并写出
,并写出![]() ,根据“
,根据“![]() ”求出x的值,再利用割补法求出面积;②设
”求出x的值,再利用割补法求出面积;②设![]() ,利用两点间距离公式分别求出AB、BM和AM的长度,再分情况进行讨论(i)当
,利用两点间距离公式分别求出AB、BM和AM的长度,再分情况进行讨论(i)当![]() 时,(ii)当
时,(ii)当![]() 时,(iii)当
时,(iii)当![]() 时,并利用勾股定理求出y的值.
时,并利用勾股定理求出y的值.
解:(1)![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
把![]() 代入
代入![]() 得
得
![]() ,
,
解得![]() ,
,
∴抛物线的解析式为![]() ;
;
(2)①![]()
![]() 的解析式为
的解析式为![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
解得,![]() (舍去)或-1,
(舍去)或-1,
![]()
在![]() 中,当
中,当![]() 时,y=4
时,y=4
![]()
![]() ,
,
![]()
②存在.
![]() 在直线
在直线![]() 上,且
上,且![]() ,
,
设![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
分三种情况:
(i)当![]() 时,有
时,有![]() ,
,
![]() ,
,
解得![]() ,
,
![]() 或
或![]() ;
;
(ii)当![]() 时,有
时,有![]() ,
,
![]() ,
,
解得![]() ;
;
![]() ,
,
(iii)当![]() 时,有
时,有![]() ,
,
![]() ,
,
解得![]() ;
;
![]() ,
,
综上,点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]() ;
;

练习册系列答案
相关题目