جâؤ؟ؤعبف
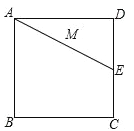
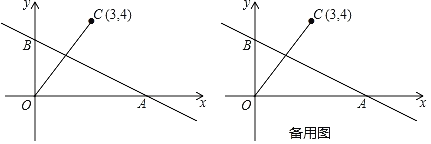
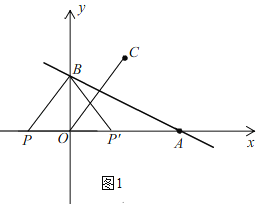
،¾جâؤ؟،؟بçح¼£¬Rt،÷OABµؤض±½ا±كOAشعxضلةد£¬±كOBشعyضلةد£¬Aµؤ×ّ±êخھ(6£¬0)£¬Bµؤ×ّ±êخھ(0£¬3)£¬شعµعز»دَدقسذز»µمCµؤ×ّ±êخھ(3£¬4)£®
£¨1£©اَض±دكABµؤ؛¯ت±ي´ïت½£»
£¨2£©Pتاxضلةدز»¶¯µم£¬µمPشعشث¶¯¹³جضذ£¬تا·ٌ´وشعؤ³¸ِخ»ضأ£¬ت¹µأ،دPBO£½،دBOC£؟بô´وشع£¬اëاَ³ِµمPµؤ×ّ±ê£»بô²»´وشع£¬اëثµأ÷ہيسة£»
£¨3£©بô¶¯µمPشعxضلةد´سµم(©پ6£¬0)³ِ·¢£¬زشأ؟أë1¸ِµ¥خ»µؤثظ¶بدٍxضلص·½دٍشث¶¯£¬¹µمP×÷ض±دكl´¹ض±سعxضل£¬ةèشث¶¯ت±¼نخھt£®اëض±½سذ´³ِµ±tخھ؛خضµت±£¬شعض±دكlةد´وشعµمM£¬شعض±دكABةد´وشعµمQ£®ت¹µأزشOCخھز»±ك£¬O£¬C£¬M£¬Qخھ¶¥µمµؤثؤ±كذخخھءâذخ£®
،¾´ً°¸،؟£¨1£©![]() £»£¨2£©´وشع£¬
£»£¨2£©´وشع£¬![]() £¬
£¬![]() »ٍ
»ٍ![]() £¬
£¬![]() £»£¨3£©1»ٍ9»ٍ
£»£¨3£©1»ٍ9»ٍ![]() »ٍ
»ٍ![]() £®
£®
،¾½âخِ،؟
£¨1£©ہûسأ´¶¨دµت·¨ض±½ساَ³ِض±دك![]() µؤ½âخِت½£»
µؤ½âخِت½£»
£¨2£©·ضµم![]() شع
شع![]() ضل¸؛°ëضلت±£¬دباَ³ِض±دك
ضل¸؛°ëضلت±£¬دباَ³ِض±دك![]() µؤ½âخِت½£¬شظإذ¶د³ِ
µؤ½âخِت½£¬شظإذ¶د³ِ![]() ئ½ذذسع
ئ½ذذسع![]() £¬½ّ¶ّاَ³ِ
£¬½ّ¶ّاَ³ِ![]() µؤ½âخِت½£¬¼´؟ةµأ³ِµم
µؤ½âخِت½£¬¼´؟ةµأ³ِµم![]() µؤ×ّ±ê£¬µم
µؤ×ّ±ê£¬µم![]() شع
شع![]() ضلص°ëضلت±£¬ہûسأ¶ش³ئذش£¬¼´؟ةµأ³ِ½لآغ£»
ضلص°ëضلت±£¬ہûسأ¶ش³ئذش£¬¼´؟ةµأ³ِ½لآغ£»
£¨3£©·ضزش![]() سë
سë![]() خھءع±ك؛حزش
خھءع±ك؛حزش![]() سë
سë![]() خھءع±كت±£¬دباَ³ِµم
خھءع±كت±£¬دباَ³ِµم![]() µؤ×ّ±ê£¬ہûسأئ½زئµؤذشضتµأ³ِµم
µؤ×ّ±ê£¬ہûسأئ½زئµؤذشضتµأ³ِµم![]() µؤ×ّ±ê£¬¼´؟ةµأ³ِ½لآغ£®
µؤ×ّ±ê£¬¼´؟ةµأ³ِ½لآغ£®
½â£؛£¨1£©ةèض±دك![]() µؤ½âخِت½خھ
µؤ½âخِت½خھ![]() £¬
£¬
![]() µم
µم![]() £¬
£¬![]() شعض±دك
شعض±دك![]() ةد£¬
ةد£¬
![]()
![]() £¬
£¬
![]()
 £¬
£¬
![]() ض±دك
ض±دك![]() µؤ½âخِت½خھ
µؤ½âخِت½خھ![]() £»
£»
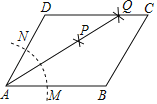
£¨2£©بçح¼1£¬
µ±µم![]() شع
شع![]() ضل¸؛°ëضلةدت±£¬
ضل¸؛°ëضلةدت±£¬
![]() µم
µم![]() £¬
£¬
![]() ض±دك
ض±دك![]() µؤ½âخِت½خھ
µؤ½âخِت½خھ![]() £¬
£¬
![]() £¬
£¬
![]() £¬
£¬
![]() £¬
£¬
![]() ض±دك
ض±دك![]() µؤ½âخِت½خھ
µؤ½âخِت½خھ![]() £¬
£¬
ءî![]() £¬شٍ
£¬شٍ![]() £¬
£¬
 £¬
£¬
![]() £¬
£¬![]() £¬
£¬
µ±µم![]() شع
شع![]() ضلص°ëضلةدت±£¬
ضلص°ëضلةدت±£¬
سة¶ش³ئذشضھ£¬![]() £¬
£¬![]() £¬
£¬
¼´µم![]() µؤ×ّ±êخھ
µؤ×ّ±êخھ![]() £¬
£¬![]() »ٍ
»ٍ![]() £¬
£¬![]() £»
£»
£¨3£©بçح¼2£¬
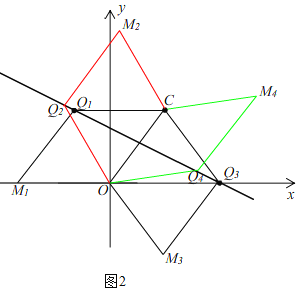
سة£¨1£©ضھ£¬ض±دك![]() µؤ½âخِت½خھ
µؤ½âخِت½خھ![]() £¬
£¬
![]() £¬
£¬
![]() £¬
£¬
ةè![]() £¬
£¬
¢ظزش![]() سë
سë![]() خھءع±كت±£¬
خھءع±كت±£¬![]() £¬
£¬
![]() £¬
£¬
![]() »ٍ
»ٍ![]() £¬
£¬
![]() £¬
£¬![]() £¬
£¬
![]() µم
µم![]() دٍ×َئ½زئ
دٍ×َئ½زئ![]() ¸ِµ¥خ»µ½µم
¸ِµ¥خ»µ½µم![]() £¬
£¬
![]() £¬
£¬
![]() µم
µم![]() ز²دٍ×َئ½زئ5¸ِµ¥خ»µأµ½µم
ز²دٍ×َئ½زئ5¸ِµ¥خ»µأµ½µم![]() £¬
£¬
![]() £¬
£¬
![]() µم
µم![]() دٍسزئ½زئ
دٍسزئ½زئ![]() ¸ِµ¥خ»£¬شظدٍدآئ½زئ
¸ِµ¥خ»£¬شظدٍدآئ½زئ![]() ¸ِµ¥خ»µ½µم
¸ِµ¥خ»µ½µم![]() £¬
£¬
![]() µم
µم![]() ز²دٍسزئ½زئ3¸ِµ¥خ»£¬شظدٍدآئ½زئ4¸ِµ¥خ»µأµ½µم
ز²دٍسزئ½زئ3¸ِµ¥خ»£¬شظدٍدآئ½زئ4¸ِµ¥خ»µأµ½µم![]() £¬
£¬
![]() £¬
£¬
¢عزش![]() سë
سë![]() خھءع±كت±£¬
خھءع±كت±£¬![]() £¬
£¬
![]()
![]() £¬
£¬
![]() »ٍ
»ٍ![]() £¬
£¬
![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬
![]() µم
µم![]() دٍ×َئ½زئ
دٍ×َئ½زئ![]() ¸ِµ¥خ»£¬شظدٍةدئ½زئ
¸ِµ¥خ»£¬شظدٍةدئ½زئ![]() ¸ِµ¥خ»µ½µم
¸ِµ¥خ»µ½µم![]() £¬
£¬![]() £¬
£¬
![]() µم
µم![]() ز²دٍ×َئ½زئ
ز²دٍ×َئ½زئ![]() ¸ِµ¥خ»£¬شظدٍةدئ½زئ
¸ِµ¥خ»£¬شظدٍةدئ½زئ![]() ¸ِµ¥خ»µ½µم
¸ِµ¥خ»µ½µم![]() £¬
£¬![]() £¬
£¬
![]() £¬
£¬
![]() µم
µم![]() دٍسزئ½زئ
دٍسزئ½زئ![]() ¸ِµ¥خ»£¬شظدٍةد
¸ِµ¥خ»£¬شظدٍةد![]() ¸ِµ¥خ»µ½
¸ِµ¥خ»µ½![]() £¬
£¬
![]() µم
µم![]() ز²دٍسزئ½زئ
ز²دٍسزئ½زئ![]() ¸ِµ¥خ»£¬شظدٍةدئ½زئ
¸ِµ¥خ»£¬شظدٍةدئ½زئ![]() ¸ِµ¥خ»µ½µم
¸ِµ¥خ»µ½µم![]() £¬
£¬![]() £¬
£¬
![]() £¬
£¬
¼´![]() µؤضµخھ1»ٍ9»ٍ
µؤضµخھ1»ٍ9»ٍ![]() »ٍ
»ٍ![]() £®
£®