Question

【题目】（发现问题）

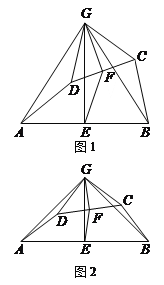
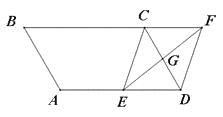
如图1，已知，以点为直角顶点，为腰向外作等腰直角、请你以为直角顶点、为腰，向外作等腰直角（不写作法，保留作图痕迹）．连接、．那么与的数量关系是________．

（拓展探究）

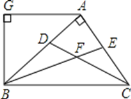
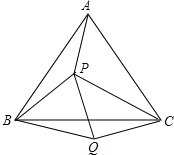
如图2，已知，以、为边向外作正方形和正方形，连接、，试判断与之间的数量关系，并说明理由．

（解决问题）

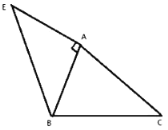
如图3，有一个四边形场地，，，，，求的最大值．

Answer 1

【答案】发现问题：BD=CE，证明见详解；拓展探究：BD=CE，证明见详解；解决问题：BD的最大值为23．

【解析】

发现问题：延长CA到M，作∠MAC的平分线AN，在AN上截取AD=AC，连接CD，即可得到等腰直角△ACD；由等腰直角三角形的性质，证出∠BAD=∠EAC，证明△BAD≌△EAC（SAS），即可得出BD=CE；

拓展探究：由正方形的性质，证出∠BAD=∠EAC，证明△BAD≌△EAC（SAS），即可得出BD=CE；

解决问题：以AB为边向外作等边三角形ABE，连接CE，由等边三角形的性质，证出△ACD是等边三角形，得出∠CAD=60°，AC=AD，证出∠BAD=∠EAC，证明△BAD≌△EAC（SAS），得出BD=CE；当C、B、E三点共线时，CE最大=BC+BE=23，得出BD的最大值为23．

发现问题：

解：延长CA到M，作∠MAC的平分线AN，在AN上截取AD=AC，连接CD，即可得到等腰直角△ACD；连接BD、CE，如图1所示：

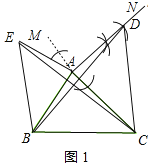
∵△ABE与△ACD都是等腰直角三角形，

∴AB=AE，AD=AC，∠BAE=∠CAD=90°，

∴∠BAD=∠EAC，

在△BAD和△EAC中，

，

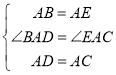∴△BAD≌△EAC（SAS），

∴BD=CE，

故答案为：BD=CE；

拓展探究：

解：BD=CE；理由如下：如图：

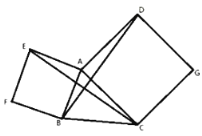
∵四边形AEFB与四边形ACGD都是正方形，

∴AB=AE，AD=AC，∠BAE=∠CAD=90°，

∴∠BAD=∠EAC，

在△BAD和△EAC中，

，

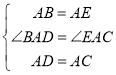∴△BAD≌△EAC（SAS），

∴BD=CE；

解决问题：

解：以AB为边向外作等边三角形ABE，连接CE，如图3所示：

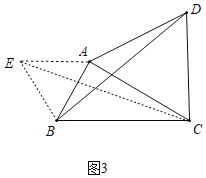
则∠BAE=60°，BE=AB=AE=8，

∵AD=CD，∠ADC=60°，

∴△ACD是等边三角形，

∴∠CAD=60°，AC=AD，

∴∠CAD+∠BAC=∠BAE+∠BAC，

即∠BAD=∠EAC，

在△BAD和△EAC中，

，

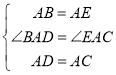∴△BAD≌△EAC（SAS），

∴BD=CE；

当C、B、E三点共线时，CE最大=BC+BE=15+8=23，

∴BD的最大值为23．