题目内容
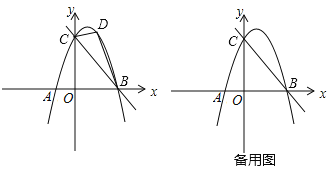
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与![]() 轴相交于A、B两点,与
轴相交于A、B两点,与![]() 轴相交于点C,OA=1,OC=3,连接BC.
轴相交于点C,OA=1,OC=3,连接BC.
(1)求b的值;
(2)点D是直线BC上方抛物线一动点(点B、C除外),当△BCD的面积取得最大值时,在![]() 轴上是否存在一点P,使得|PB﹣PD|最大,若存在,请求出点P的坐标;若不存在,请说明理由.
轴上是否存在一点P,使得|PB﹣PD|最大,若存在,请求出点P的坐标;若不存在,请说明理由.
(3)在(2)的条件下,若在平面上存在点Q,使得以点B、C、D、Q为顶点的四边形为平行四边形,请直接写出点Q坐标.
【答案】(1)b=2,c=3;(2)P(0,![]() );(3) (-
);(3) (-![]() ,
,![]() ),(
),(![]() ,-
,-![]() ),(
),(![]() ,
,![]() ),
),
【解析】
(1)根据OA=1,OC=3得出点A和C的坐标,代入抛物线的解析式列方程组可得b的值;(2)写出抛物线的解析式,利用三角形面积公式可知,当底边BC一定时,高最大时其△BCD的面积最大,即作BC的平行线,其平行线的距离最大时,即平行线l与抛物线有一个交点时,交点为D,利用方程组的解可得D的坐标,最后根据三角形的三边关系确定当P、B、D三点共线时,|PB﹣PD|最大,利用待定系数法求直线BD的解析式,与y轴的交点就是点P;(3)如图4,画出平行四边形,有三种情况:根据平移规律确定Q的坐标.
(1)∵OA=1,OC=3,
∴A(-1,0),C(0,3),
把A(-1,0),C(0,3)代入抛物线y=-x2+bx+c中得:
∵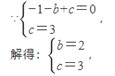 ,
,
(2)由(1)得:抛物线y=-x2+2x+3,
当y=0时,-x2+2x+3=0,
解得:x=-1或3,
∴B(3,0),
设直线BC的解析式为:y=kx+b,
 ,
,
∴直线BC的解析式为:y=-x+3,
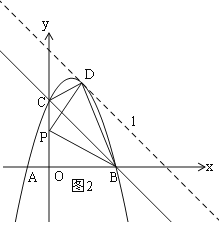
如图1,作直线l∥BC,
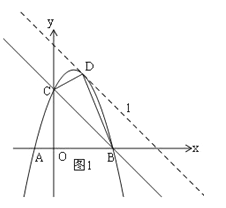
设直线l的解析式为:y=-x+b,
由题意可知:△BCD中边BC长一定,当△BCD的面积取得最大值时,即以BC为底边,其高最大,
也就是直线l与抛物线有一个交点时,三角形高最大,△BCD的面积最大,
则![]() ,
,
-x2+2x+3=-x+b,
x2-3x+b-3=0,
△=(-3)2-4×1×(b-3)=0, ,
,
∵P是y轴上任意一点,
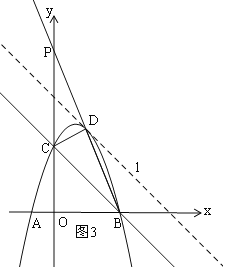
如图2,|PB-PD|<BD,
∴当P、B、D三点共线时,|PB-PD|最大,如图3,
(3)如图4,分三种情况:
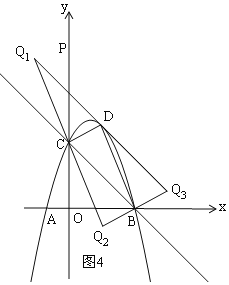
①当CD为平行四边形的对角线时,

 巧学巧练系列答案
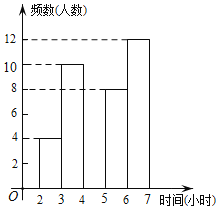
巧学巧练系列答案【题目】某中学为了了解学生每周在校体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) | 频数(人数) | 频率 |
2≤t<3 | 4 | 0.1 |
3≤t<4 | 10 | 0.25 |
4≤t<5 | a | 0.15 |
5≤t<6 | 8 | b |
6≤t<7 | 12 | 0.3 |
合计 | 40 | 1 |
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?