题目内容
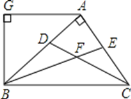
【题目】如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,AG⊥BG,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°.其中正确的结论是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
由已知条件可知∠ABC+∠ACB=90°,又因为CD、BE分别是△ABC的角平分线,所以得到∠FBC+∠FCB=45°,所以求出∠CFB=135°;有平行线的性质可得到:∠ABG=∠ACB,∠BAG=2∠ABF.所以可知选项①③④正确.
解:∵AB⊥AC.
∴∠BAC=90°,
∵∠BAC+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=90°
∵CD、BE分别是△ABC的角平分线,
∴2∠FBC+2∠FCB=90°
∴∠FBC+∠FCB=45°
∴∠BFC=135°故④正确.
∵AG∥BC,
∴∠BAG=∠ABC
∵∠ABC=2∠ABF
∴∠BAG=2∠ABF 故①正确.
∵AB⊥AC,
∴∠ABC+∠ACB=90°,
∵AG⊥BG,
∴∠ABG+∠GAB=90°
∵∠BAG=∠ABC,
∴∠ABG=∠ACB 故③正确.
故选:C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目