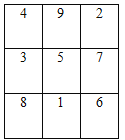
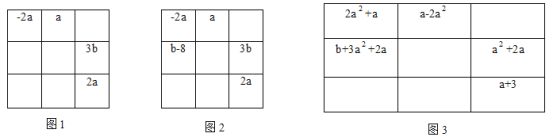
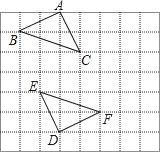
题目内容
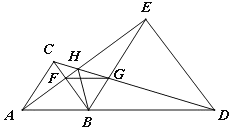
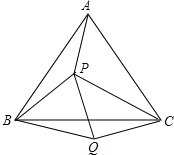
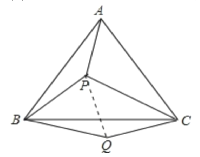
【题目】如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
(1) 观察并猜想AP与CQ之间的大小关系,并证明你的结论;
(2) 若PA:PB:PC=3:4:5,连接PQ,试判断△PQC的形状,并说明理由.
【答案】(1)AP=CQ,证明见解析(2)△PQC是直角三角形,证明见解析
【解析】
根据等边三角形的性质利用SAS判定△ABP≌△CBQ,从而得到AP=CQ;设PA=3a,PB=4a,PC=5a,由已知可判定△PBQ为正三角形从而可得到PQ=4a,再根据勾股定理判定△PQC是直角三角形.
(1)猜想:AP=CQ,
证明:∵∠ABP+∠PBC=60°,∠QBC+∠PBC=60°,
∴∠ABP=∠QBC.
又AB=BC,BP=BQ,
∴△ABP≌△CBQ,
∴AP=CQ;
(2)由PA:PB:PC=3:4:5,
可设PA=3a,PB=4a,PC=5a,
连接PQ,在△PBQ中
由于PB=BQ=4a,且∠PBQ=60°,
∴△PBQ为正三角形.
∴PQ=4a.
于是在△PQC中
∵PQ![]() +QC
+QC![]() =16a
=16a![]() +9a
+9a![]() =25a
=25a![]() =PC
=PC![]()
∴△PQC是直角三角形.

练习册系列答案
相关题目