题目内容
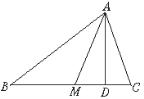
【题目】如图,在△ABC中,AM是中线,AD是高线.
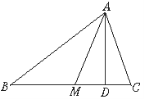
(1)若AB比AC长4 cm,则△ABM的周长比△ACM的周长多__________ cm.
(2)若△AMC的面积为12 cm2,则△ABC的面积为__________cm 2.
(3)若AD又是△AMC的角平分线,∠AMB=130°,求∠ACB的度数.(写过程)
【答案】(1)4;(2)24;(3)50°
【解析】
(1) △ABM的周长与△ACM的周长的差,实际为AB与AC的差;
(2)因为BC=2CM.所以△A BC的面积是△AMC的面积的2倍;
(3)由∠AMB=130°,易得∠AMD=50°,又AD既是高,又是角平分线,易得△ADM≌△ADC,∠AMC=∠ACB=50°
解: (1) : △ABM的周长为:AB+ BM+AM,△ACM的周长为AC+CM+AM,
∵AM是△ABC中线
∴BM=CM, BC=2CM
∴△ABM的周长-△ACM的周长为:(AB+ BM+AM )-(AC+CM+AM)=AB-AC=4(cm)
故答案为: 4;
(2) ∵ ![]()
∴![]()
故答案为: 24;
(3)
解: ∵ AD是高线
∴∠ADM=∠ADC=90°
∵ AD又是△AMC的角平分线
∴ ∠MAD=∠CAD
∵在△ADM和△ADC中
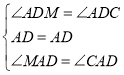
∴ △ADM≌△ADC (SAS)
∴∠AMD=∠ACD
∵ ∠AMB=130°
∴∠AMD=50°
∴∠ACB =50°

练习册系列答案
相关题目