题目内容
【题目】抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .已知点
.已知点![]() ,点
,点![]() .
.
(1)当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
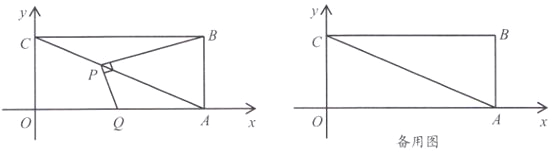
(2)直线![]() 与抛物线交于
与抛物线交于![]() 两点,抛物线的对称轴为直线
两点,抛物线的对称轴为直线![]()
①求![]() ,
,![]() 所满足的数量关系式;
所满足的数量关系式;
②当OP=OA时,求线段![]() 的长度.
的长度.
【答案】(1)(![]() ,0);(2)①
,0);(2)①![]() ;②
;②![]() 或
或![]() .
.
【解析】
(1)利用待定系数法,将![]() ,点
,点![]() ,
,![]() 代入函数解析式,求得
代入函数解析式,求得![]() ,从而求得函数解析式及对称轴,然后根据数轴上的对称性求得点B的坐标;
,从而求得函数解析式及对称轴,然后根据数轴上的对称性求得点B的坐标;
(2)①由抛物线的对称轴求得![]() ,求得
,求得![]() ,然后将点
,然后将点![]() ,点
,点![]() 代入函数解析式求得p与a的数量关系;
代入函数解析式求得p与a的数量关系;
②由OP=OA时,分情况讨论当P(0,1)或(0,-1),求得p的值,从而确定二次函数和一次函数解析式,然后求其交点坐标,利用勾股定理求PN的长度.
解:(1)将点![]() ,点
,点![]() 代入函数解析式,得
代入函数解析式,得![]()
当![]() 时,可得
时,可得![]() ,解得:
,解得:![]()
∴此时抛物线解析式为:![]() ,抛物线对称轴为
,抛物线对称轴为![]()
设B点坐标为(x,0) ,则此时![]() ,解得:
,解得:![]()
∴B点坐标为(![]() ,0)
,0)
(2)①将点![]() ,点
,点![]() 代入函数解析式,得
代入函数解析式,得![]()
有题意可知:![]() ,则
,则![]()
∴![]() ,解得
,解得![]()
②当OP=OA时,P(0,1)或(0,-1)
当P(0,1)时,-p=1,即p=-1,则![]() ,解得
,解得![]()
∴此时抛物线解析式为:![]()
又∵直线![]() 与抛物线交于
与抛物线交于![]() 两点
两点
∴一次函数解析式为:![]()
由此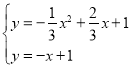 ,解得
,解得![]() 或
或![]()
∴此时P(0,1)),N(5,-4)
∴PN=![]()
当P(0,-1)时,-p=-1,即p=1,则![]() ,解得
,解得![]()
∴此时抛物线解析式为:![]()
又∵直线![]() 与抛物线交于
与抛物线交于![]() 两点
两点
∴一次函数解析式为:![]()
由此 ,解得
,解得![]() 或
或![]()
∴此时P(0,-1)),N(-1,0)
∴PN=![]()
∴综上所述,PN的长度为![]() 或
或![]() .
.

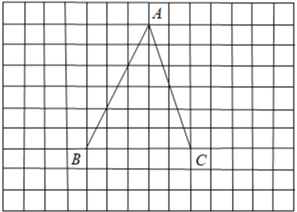
【题目】数学活动课上,张老师引导同学进行如下探究:如图1,将长为![]() 的铅笔
的铅笔![]() 斜靠在垂直于水平桌面
斜靠在垂直于水平桌面![]() 的直尺
的直尺![]() 的边沿上,一端
的边沿上,一端![]() 固定在桌面上,图2是示意图.
固定在桌面上,图2是示意图.
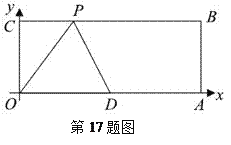
活动一
如图3,将铅笔![]() 绕端点
绕端点![]() 顺时针旋转,
顺时针旋转,![]() 与
与![]() 交于点
交于点![]() ,当旋转至水平位置时,铅笔
,当旋转至水平位置时,铅笔![]() 的中点
的中点![]() 与点
与点![]() 重合.
重合.
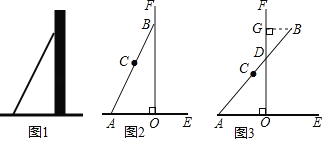
数学思考
(1)设![]() ,点
,点![]() 到
到![]() 的距离
的距离![]() .
.
①用含![]() 的代数式表示:
的代数式表示:![]() 的长是_________
的长是_________![]() ,
,![]() 的长是________
的长是________![]() ;
;
②![]() 与
与![]() 的函数关系式是_____________,自变量
的函数关系式是_____________,自变量![]() 的取值范围是____________.
的取值范围是____________.
活动二
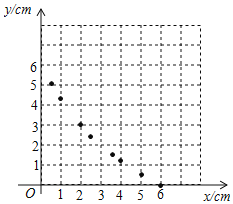
(2)①列表:根据(1)中所求函数关系式计算并补全表格.
| 6 | 5 | 4 | 3.5 | 3 | 2.5 | 2 | 1 | 0.5 | 0 |
| 0 | 0.55 | 1.2 | 1.58 | 1.0 | 2.47 | 3 | 4.29 | 5.08 |
②描点:根据表中数值,描出①中剩余的两个点![]() .
.
③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象.
数学思考
(3)请你结合函数的图象,写出该函数的两条性质或结论.