题目内容
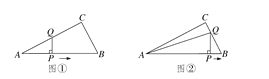
【题目】如图,在平面直角坐标系中,已知矩形OABC的顶点A在x轴上,顶点C在y轴上,OA=8,OC=4.点P为对角线AC 上一动点,过点P作PQ⊥PB,PQ交x轴于点Q.
(1)tan∠ACB=________;
(2)在点P从点C运动到点A的过程中,![]() 的值是否发生变化?如果变化,请求出其变化范围;如果不变,请求出其值;
的值是否发生变化?如果变化,请求出其变化范围;如果不变,请求出其值;
(3)若将△QAB沿直线BQ折叠后,点A与点P重合,则PC的长为________
【答案】(1)![]() ;(2)
;(2) ![]() 的值不变,等于
的值不变,等于![]() ,理由见解析;(3)
,理由见解析;(3)![]()
【解析】
(1)根据tan∠ACB=![]() 即可求解;
即可求解;
(2)过点P分别作PD⊥OA于点D、PE⊥AB于点E,然后证明△PDQ∽△PEB,再求出![]()
(3)连接BQ、交CA于点H,由折叠可知BQ垂直平分AP,易证得△BAH∽△CAB, 又有AB=4、BC=8,进而可得AH、AC的长,据此解答即可.
(1)根据tan∠ACB=![]()
(2)解:在点P从点C运动到点A的过程中,![]() 的值不变,等于
的值不变,等于![]() ,
,
如图1,过点P分别作PD⊥OA于点D、PE⊥AB于点E,根据
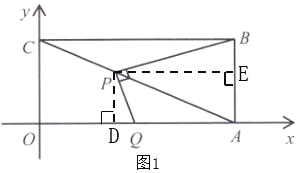
∵∠PDA=∠PEA=∠BAO=90°,
∴四边形PDAE是矩形,
∴PD=AE,PE=AD,∠EPF=90°,
又∵PQ⊥PB,
∴∠BPQ=90°,
∴∠DPQ=∠EPB,
∴△PDQ∽△PEB,
∴![]() .
.
又∵![]() ,
,
∴ 在点P从点C运动到点A的过程中,![]() 的值不变,等于
的值不变,等于![]() .
.
(3)![]()

连接BQ,BQ与AC交于H点,
在直角三角形ABC中,根据勾股定理求得AC=![]()
∵△QAB沿直线BQ折叠后,A与P重合,
∴BQ是四边形AQPB的对称轴,
∴BQ垂直平分AP.
∵BH⊥AC,
∴∠BHA=∠ABC=90°,
又∠BAC是公共角,
∴△BAH∽△CAB,
∴AB2=AH·AC,
∴42= AH·![]()
∴AH=![]() ,
,
∴AP=2AH=![]() ,
,
∴PC=AC-AP=![]() .
.