题目内容
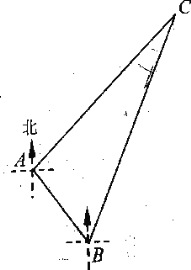
【题目】如图,⊙O是△ABC的外接圆,AB为直径, OD∥BC交⊙O于点D,交AC于点E,连接AD,BD,CD.
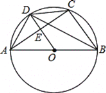
(1)求证:AD=CD;
(2)若AB=10,cos∠ABC=![]() ,求tan∠DBC的值.
,求tan∠DBC的值.
【答案】(1)详见解析;(2)tan∠DBC=![]() .
.
【解析】
(1)由AB为直径,OD∥BC,易得OD⊥AC,然后由垂径定理证得,![]() =
=![]() ,继而证得结论;
,继而证得结论;
(2)由AB=10,cos∠ABC=![]() ,可求得OE的长,继而求得DE,AE的长,则可求得tan∠DAE,然后由圆周角定理,证得∠DBC=∠DAE,则可求得答案.
,可求得OE的长,继而求得DE,AE的长,则可求得tan∠DAE,然后由圆周角定理,证得∠DBC=∠DAE,则可求得答案.
(1)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∵OD∥BC,
∴∠AEO=∠ACB=90°,
∴OD⊥AC,
∴![]() =
=![]() ,
,
∴AD=CD;
(2)解:∵AB=10,
∴OA=OD=![]() AB=5,
AB=5,
∵OD∥BC,
∴∠AOE=∠ABC,
在Rt△AEO中,OE=OAcos∠AOE=OAcos∠ABC=5×![]() =3,
=3,
∴DE=OD=OE=5﹣3=2,
∴AE=![]() =
=![]() =4,
=4,
在Rt△AED中,tan∠DAE=![]() =
=![]() =
=![]() ,
,
∵∠DBC=∠DAE,
∴tan∠DBC=![]() .
.

【题目】某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A、B、C、D四等,并绘制成下面的频数分布表和扇形统计图
等级 | 成绩(得分) | 频数(人数) | 频率 |
A | 9~10分 | x | m |
B | 8~7 | 23 | 0.46 |
C | 6~5 | y | n |
D | 5分以下 | 3 | 0.06 |
(1)试直接写出x,y,m,n的值;
(2)求表示得分为C等的扇形的圆心角的度数;
(3)如果该校九年级共有男生400名,试估计这400名男生中成绩达到A等和B等的人数共有多少人?

【题目】某校九年级开展“光盘行动”宣传活动,各班级参加该活动的人数统计结果如下表,对于这组统计数据,下列说法中正确的是()
班级 | 1班 | 2班 | 3班 | 4班 | 5班 | 6班 |
人数 | 52 | 60 | 62 | 54 | 58 | 62 |
A.平均数是58B.中位数是58C.极差是40D.众数是60