题目内容
【题目】某校九年级开展“光盘行动”宣传活动,各班级参加该活动的人数统计结果如下表,对于这组统计数据,下列说法中正确的是()
班级 | 1班 | 2班 | 3班 | 4班 | 5班 | 6班 |
人数 | 52 | 60 | 62 | 54 | 58 | 62 |
A.平均数是58B.中位数是58C.极差是40D.众数是60
【答案】A
【解析】
分别根据平均数,中位数,极差,众数的计算方法计算即可作出判断
平均数是指在一组数据中所有数据之和再除以数据的个数,因此,这组数据的平均数是:
![]() .
.
中位数是一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数).由此将这组数据重新排序为52,54,58,60,62,62,∴中位数是按从小到大排列后第3,4个数的平均数为:59.
根据一组数据中的最大数据与最小数据的差叫做这组数据的极差的定义,这组数据的极差是:
62-52=10.
众数是在一组数据中,出现次数最多的数据,这组数据中,出现次数最多的是62,故这组数据的众数为62.
综上所述,说法正确的是:平均数是58.故选A.

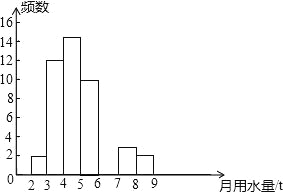
【题目】小亮同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了若干户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图)
月均用水量(单位:t) | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | a | b |
5≤x<6 | 10 | 20% |
6≤x<7 | c | 12% |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |
(1)频数分布表中a= ,b= .(填百分比),c= ;补全频数分布直方图.
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有 户;
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,请用列表法或画树状图求抽取出的2个家庭来自不同范围的概率.